Ответы
Ответ дал:
0
y=1/3* x^3 - 9x - 7
y ' = 1/3 *3x^2 - 9 = x^2 - 9
y ' = 0
x^2 - 9 = 0
( x - 3)( x + 3) =0
x = ± 3
+ - +
------------------*----------------*--------------->
( - 3) (3)
т. max ==> x = - 3
y ' = 1/3 *3x^2 - 9 = x^2 - 9
y ' = 0
x^2 - 9 = 0
( x - 3)( x + 3) =0
x = ± 3
+ - +
------------------*----------------*--------------->
( - 3) (3)
т. max ==> x = - 3
Ответ дал:
0
производная

нашли стационарные точки, смотрим таблицу во вложении
ответ -3
нашли стационарные точки, смотрим таблицу во вложении
ответ -3
Приложения:
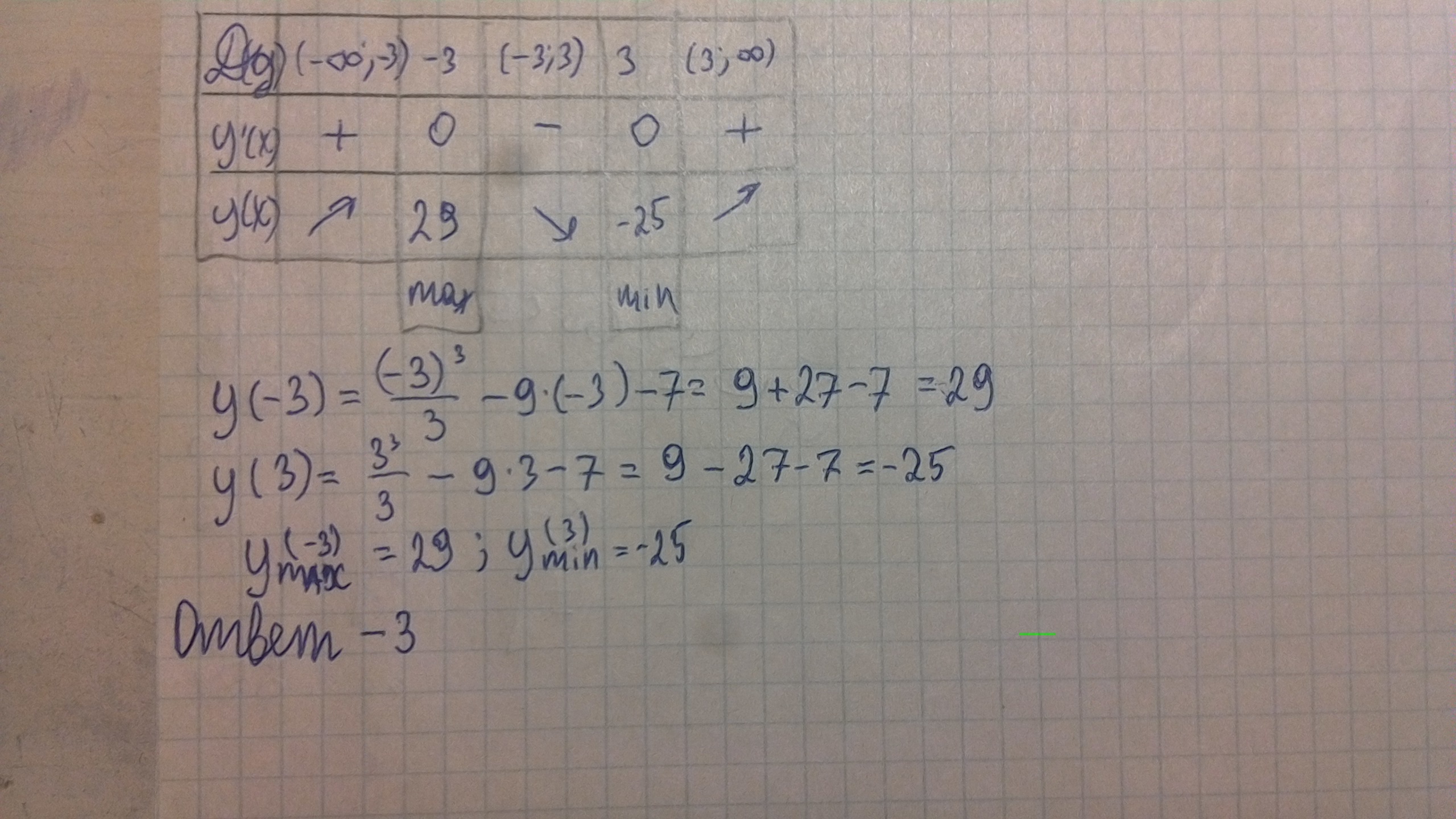
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад