Из пяти точек никакие три не лежат на одной прямой. Сколько различных треугольников с вершинами в этих точках можно построить?
Ответы
Ответ дал:
0
Количество треугольников определяется числом сочетаний
из 5 элементов по 3:

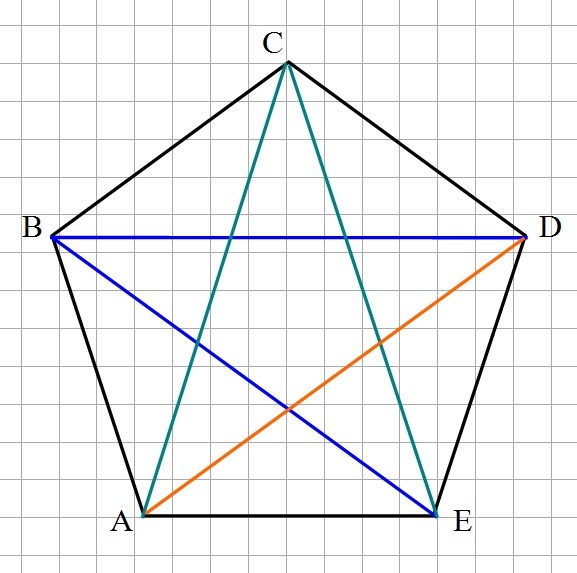
Для иллюстрации - см. рис.
Треугольники:
ABC; ABD; ABE; BCD; BCE; CDA; CDE; BDE; ADE; ACE
Всего 10.
из 5 элементов по 3:
Для иллюстрации - см. рис.
Треугольники:
ABC; ABD; ABE; BCD; BCE; CDA; CDE; BDE; ADE; ACE
Всего 10.
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад