можно ли на плоскости отметить 10 точек так чтобы любые три из них были вершинами тупоугольного треугольника
Ответы
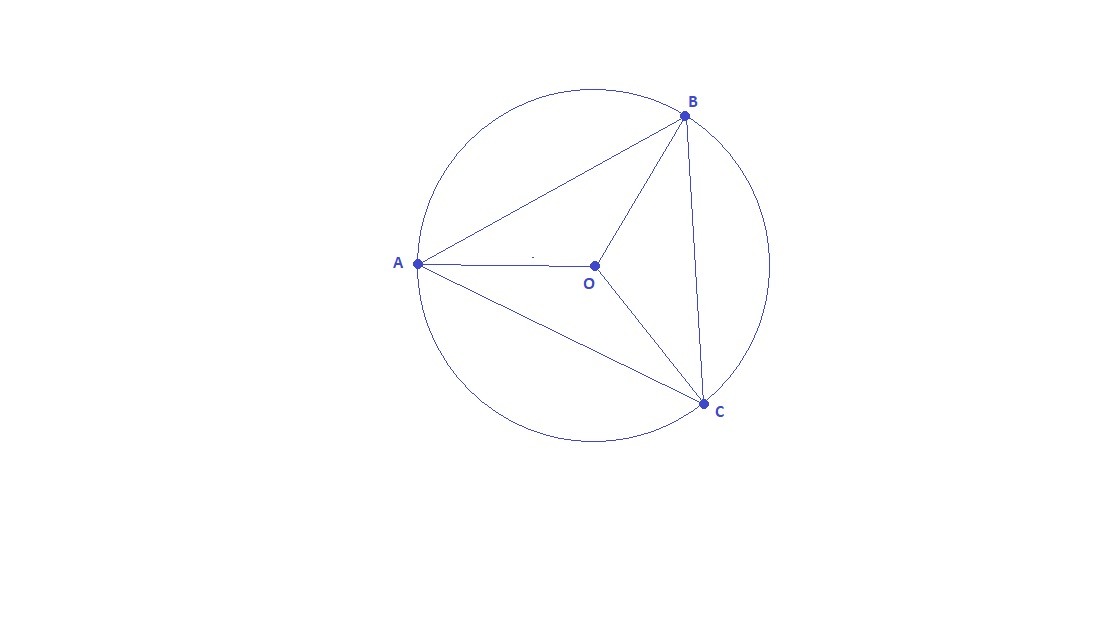
Поскольку расстояние между точками не имеет значения, а важны только углы, рассмотрим окружность.
Первая точка О - центр окружности. Разместим 3 точки на окружности так, чтобы радиусы образовали тупые углы. Четвертую точку на окружности с соблюдением тех же условий разместить не удастся, так как полный угол составляет 360°, а если его разделить на 4 угла, то только 3 могут быть тупыми, а четвертый - обязательно острый (в крайнем случае - все прямые).
Но и при таком расположении точек А, В и С на окружности каждый вписанный угол АВС, ВАС и АСВ будет острым, так как вписанный равен половине центрального:
180° > ∠AOB > 90°
∠ACB = 1/2 ∠AOB, ⇒ 90° > ∠ACB > 45°
Т.е. даже 4 точки разместить так, чтобы любые три из них были вершинами тупоугольного треугольника нельзя.