1. Отрезок AB – диаметр окружности. Прямая AT – касательная к окружности, а прямая BT пересекает окружность в точке C. Вычислите градусные меры углов треугольника ATC, если известно, что градусная мера дуги AC равна 80°.
Ответы
Ответ дал:
0
∠ACB - вписанный и опирается на дугу AB. Т.к. AB - диаметр окружности, то ∪AB=180° и ∠ACB=180/2=90° ⇒ ∠ACT=90° как смежный угол.
∪BC=∪AB-∪AC=180-80=100°. ∠BAC вписанный и опирается на дугу BC ⇒ ∠BAC=100/2=50°
По свойству касательной к окружности ∠BAT=90° ⇒ ∠CAT=90-50=40°
∠ATC=180-(40+90)=50°
Ответ: ∠ATC=50°; ∠ACT=90°; ∠CAT=40°
∪BC=∪AB-∪AC=180-80=100°. ∠BAC вписанный и опирается на дугу BC ⇒ ∠BAC=100/2=50°
По свойству касательной к окружности ∠BAT=90° ⇒ ∠CAT=90-50=40°
∠ATC=180-(40+90)=50°
Ответ: ∠ATC=50°; ∠ACT=90°; ∠CAT=40°
Приложения:
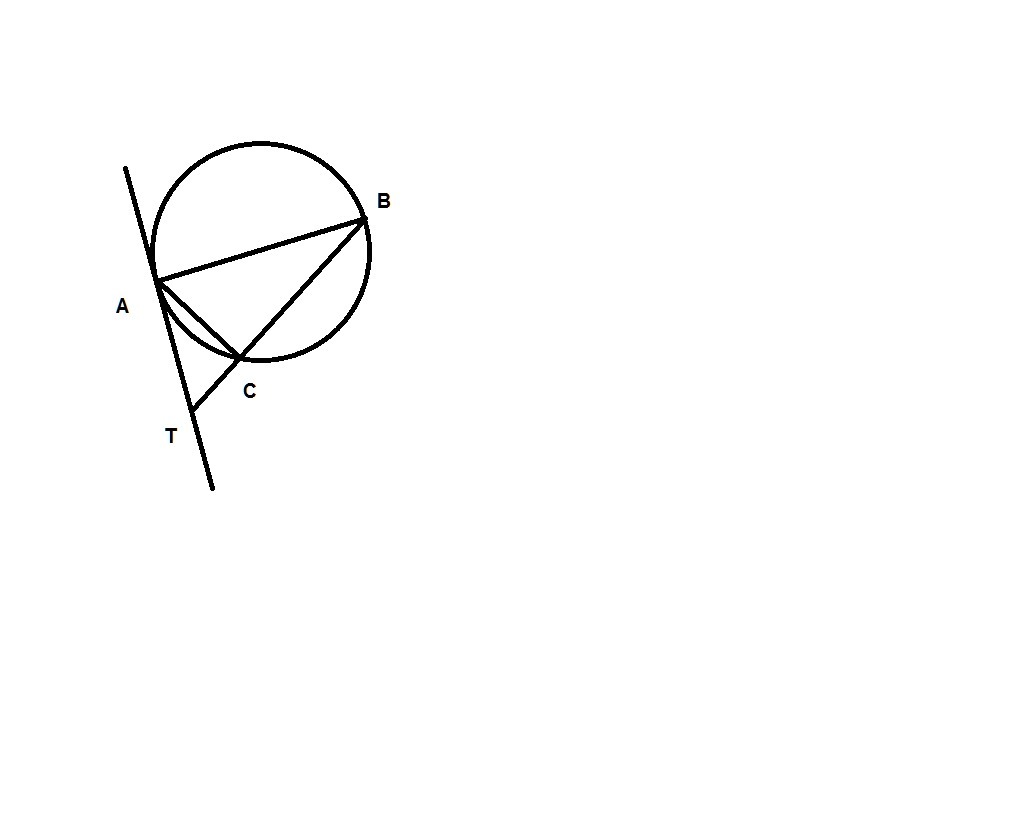
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад