Question

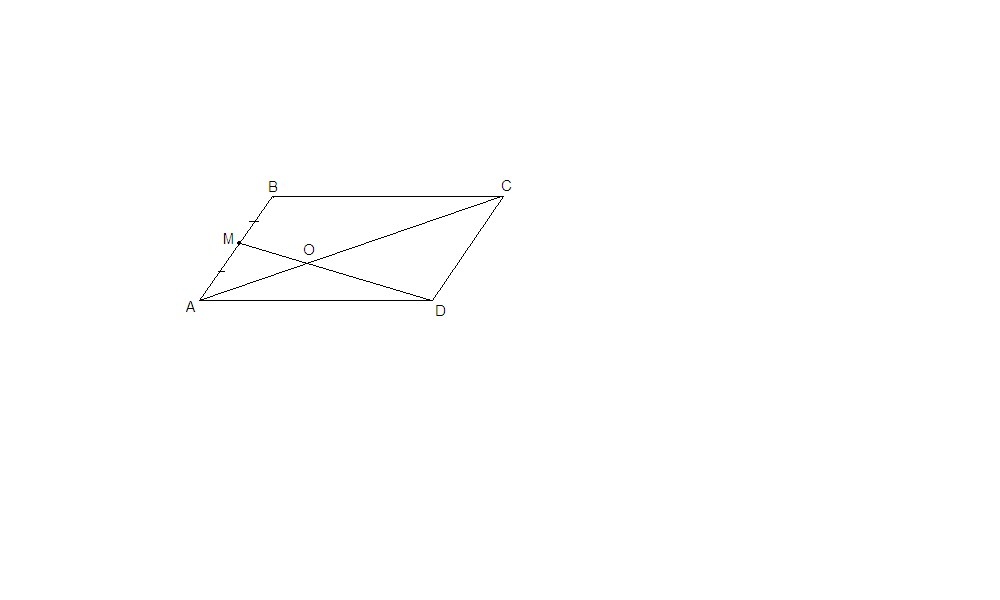
В параллелограмме ABCD A C равно 15 см середина М стороны AB соединена отрезком c вершиной D Найдите отрезки на которыe DM делит диагональ AC

Answer 1

ΔАОМ подобен ΔCOD по двум углам: углы при вершине О равны как вертикальные, ∠МАО = ∠DCO как накрест лежащие при пересечении параллельных АВ и CD секущей АС.

АМ = АВ/2
В параллелограмме противоположные стороны равны, значит
АМ = CD/2
Тогда
АО : ОС = АМ : CD = 1 : 2
AO = AC/3 = 15/3 = 5 см
ОС = 15 - 5 = 10 см