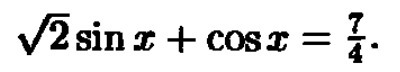Ответы
Ответ дал:
0
Ответ&/'&/-*/'*%#*/#(_"(^"*^'₩€=#€%
Приложения:

Ответ дал:
0
task/25892645
------------------
√2sinx +cosx = 7/4 ;
* * * asinα+bcosα =√(a²+b²) sin(α +φ) ,где φ =arctg(b/a) * * *
√3sin(x +arctg(1/√2) = 1,75 ;
sin(x +arctg(1/√2) =1,75/ √3 > 1 →нет решения * * * √3 ≈1,733 * * *
* * * * * * * * * * * * *
asinα+bcosα =√(a²+b²) (a /√(a²+b²)*sinα +b /√(a²+b²)*cosα ) =
|| ( a /√(a²+b²) )² + ( b/√(a²+b²) )² =1 ||
√(a²+b²) (cosφ*sinα +sin φ*cosα ) =√(a²+b²)sin(α +φ) , где
cosφ = a /√(a²+b²) , sin φ =b /√(a²+b²) ⇒tgφ =b/a * * *
------------------
√2sinx +cosx = 7/4 ;
* * * asinα+bcosα =√(a²+b²) sin(α +φ) ,где φ =arctg(b/a) * * *
√3sin(x +arctg(1/√2) = 1,75 ;
sin(x +arctg(1/√2) =1,75/ √3 > 1 →нет решения * * * √3 ≈1,733 * * *
* * * * * * * * * * * * *
asinα+bcosα =√(a²+b²) (a /√(a²+b²)*sinα +b /√(a²+b²)*cosα ) =
|| ( a /√(a²+b²) )² + ( b/√(a²+b²) )² =1 ||
√(a²+b²) (cosφ*sinα +sin φ*cosα ) =√(a²+b²)sin(α +φ) , где
cosφ = a /√(a²+b²) , sin φ =b /√(a²+b²) ⇒tgφ =b/a * * *
Вас заинтересует
1 год назад
1 год назад
2 года назад
3 года назад
8 лет назад