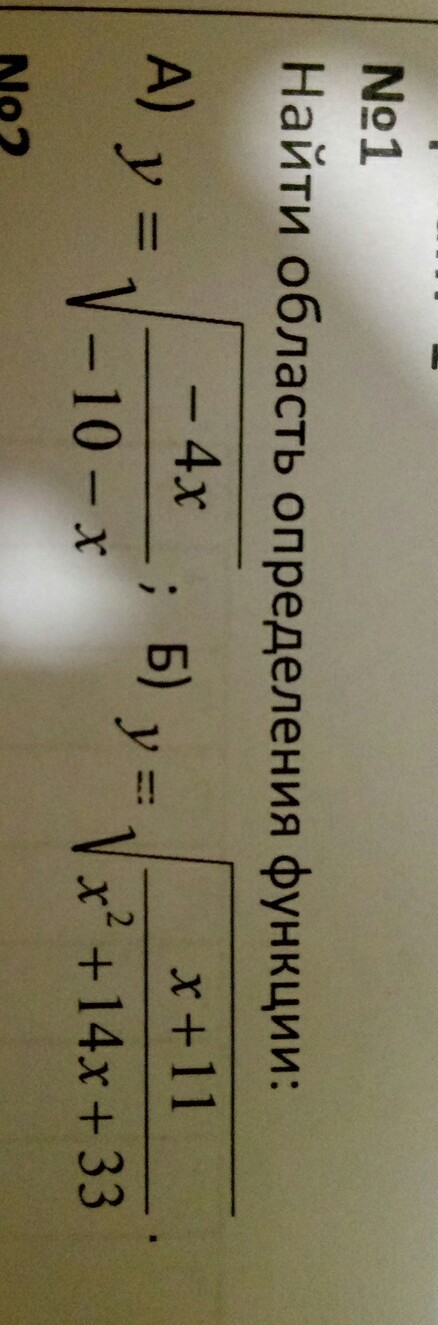Ответы
Ответ дал:
0
A)

+ | - | +
| |
| |
..........(-10)................. 0..................

B)

- | + | - | +
| | |
..........(-18)...................-11.............(-10)..............
![t \in (-18;-11] \cup (-10; +\infty)\\ t \in (-18;-11] \cup (-10; +\infty)\\](https://tex.z-dn.net/?f=t+%5Cin+%28-18%3B-11%5D+%5Ccup+%28-10%3B+%2B%5Cinfty%29%5C%5C)
+ | - | +
| |
| |
..........(-10)................. 0..................
B)
- | + | - | +
| | |
..........(-18)...................-11.............(-10)..............
Вас заинтересует
1 год назад
2 года назад
3 года назад
3 года назад
9 лет назад