Question

Y=|4-(х- 2) в квадрате|-1 построить график функции и определить, при каких значениях с прямая у=с имеет с графиком две общие точки. Я не понимаю что с модулем делать, подскажите как модуль раскрыть и всё.

Answer 1

$y=|4-(x-2)^2|-1 \\ \\ y=|4-x^2+4x-4|-1 \\ y=|-x^2+4x|-1$

найдем нули подмодульного выражения
$-x^2+4x=0 \\ x^2-4x=0 \\ x(x-4)=0 \\ x=0 \cup x=4$
тогда точки 0 и 4 являются точками смены знака открытия модуля.

y=$\left \{ {{-x^2+4x-1;x \in(0;4)} \atop {x^2-4x-1;x\in(-\infty;0]\cup[4;+\infty)}} \right.$

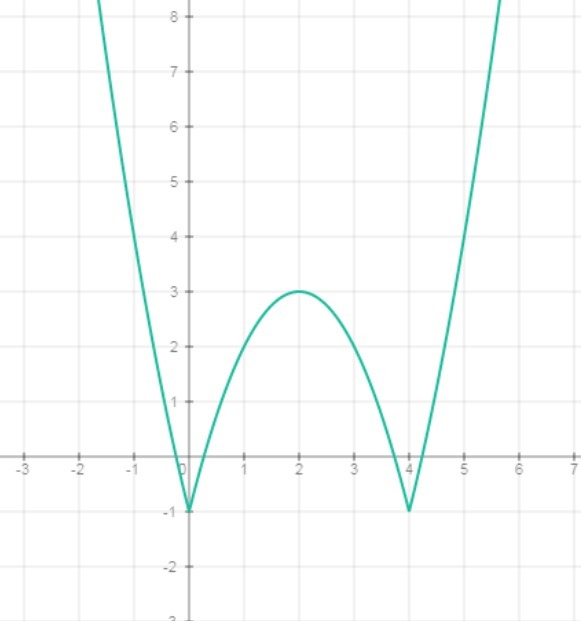
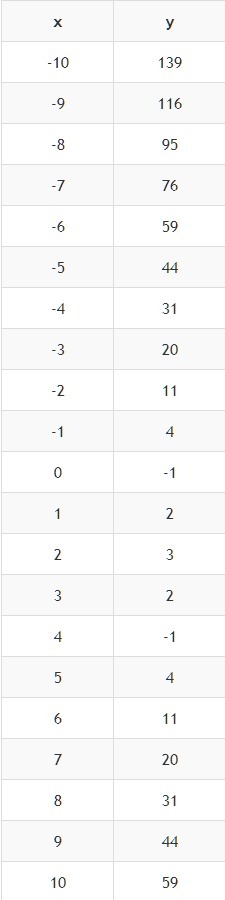
Построение графика выполняем по точкам.

Прямая y=c будет иметь с графиком ровно 2 общие точки, если будет проходить выше вершины параболы y=-x²+4x-1, значит
$c\ \textgreater \ \dfrac{4-16}{-4} \\ c\ \textgreater \ 3$

Ответ: прямая y=c имеет ровно 2 общие точки с графиком при c∈(3;+∞)