Помогите пожалуйста. Исследовать знакопеременные ряды на условную или абсолютную сходимость.
Приложения:
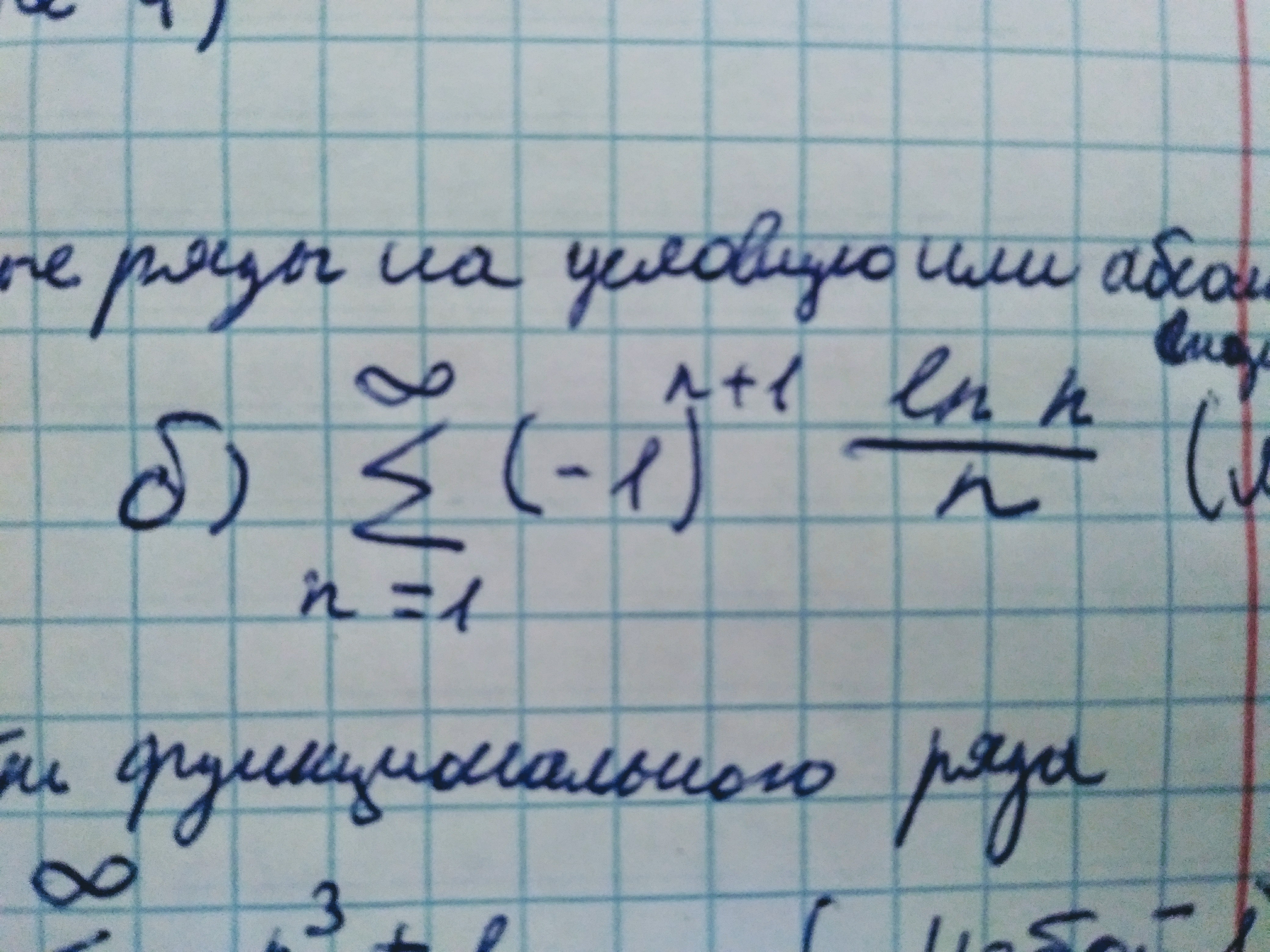
Ответы
Ответ дал:
0
По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, но в нашем случае для данного ряда не выполняется.
То есть, ряд будет расходится.
То есть, ряд будет расходится.
Ответ дал:
0
Это я понимаю, если можно решение до этого момента
Ответ дал:
0
какой в самом начале нужно использовать признак?
Ответ дал:
0
геть
Ответ дал:
0
Признак Лейбница выполняется:
Начиная с 3-го номера члены ряда убывают по абсолютной величине.
(В формулировке признака сказано, что члены ряда из абсолютных величин должны убывать, начиная с некоторого номера.)
Знакочередующийся ряд сходится по признаку Лейбница, то есть условно.
Проверим на абсолютную сходимость.
По интегральному признаку сходимости:
Несобственный интеграл расходится, значит и ряд из абсолютных величин расходится.
Поэтому у знакочередующегося ряда не будет абсолютной сходимости, но, как мы проверили, есть условная сходимость.
Ответ дал:
0
Спасибо вам большое
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад