Question

ABCD-параллелограмм. PMNKP=20см. Найти MN,MP

Answer 1

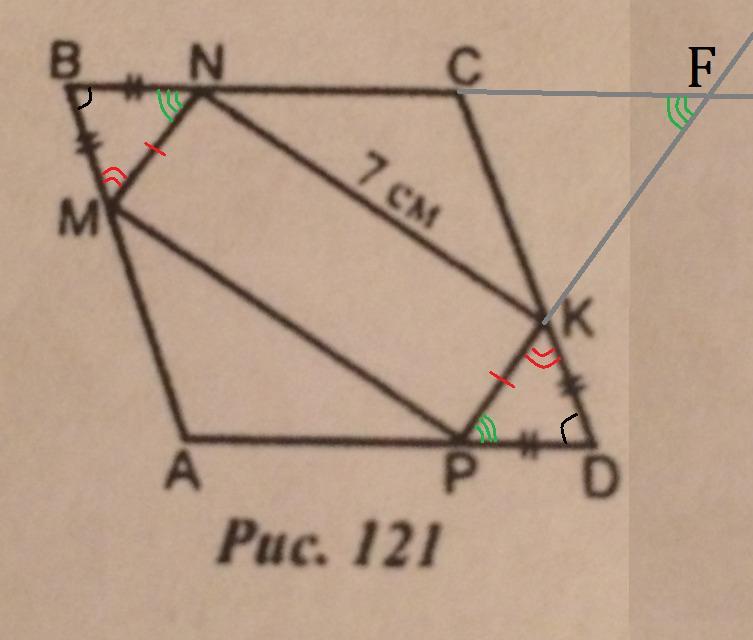
В параллелограмме противоположные стороны равны и параллельны, а противоположные углы равны, поэтому ∠MBN=∠KDP и BC║AD.

ΔBMN=ΔDKP (по двум сторонам и углу между ними) у равных треугольников соответственные элементы равны, то есть MN=KP и ∠BNM=∠DPK. Продлим сторону стороны PK и BC как показано на рисунке, PK∩BC=F. ∠DPK=∠BFK как внутренние накрест лежащие углы при параллельных прямых PD, BF и секущей PF. ∠MNB=∠KFC, при этом это соответственные углы при прямых MN, KF и секущей NF, поэтому MN║KF; MN║PK как отрезки принадлежащие параллельным прямым.

MNKP - параллелограмм т.к. MN=PK и MN║PK.

$P_{MNKP}=20cm;;MP=NK=7cm;MN=PK\\2MN+2NK=P_{MNKP}=20cm;|:!2\MN+NK=MN+7cm=10cmRightarrow MN=3cm.\\Otvet :;MN=3cm,;MP=7cm.$