Question

В правильной четырехугольной призме ABCDA1B1C1D1 сторона основания равна 8, а боковое ребро 4 корня из 2. На ребрах BC и C1D1 отмеченных точки K и L, так что BK=C1L=2. Плоскость y параллельная прямой BD и содержит точки K и L.
Найдите расстояние от точки B до плоскости Y.
Решить задачу векторным способом. Желательно подробно.

Answer 1

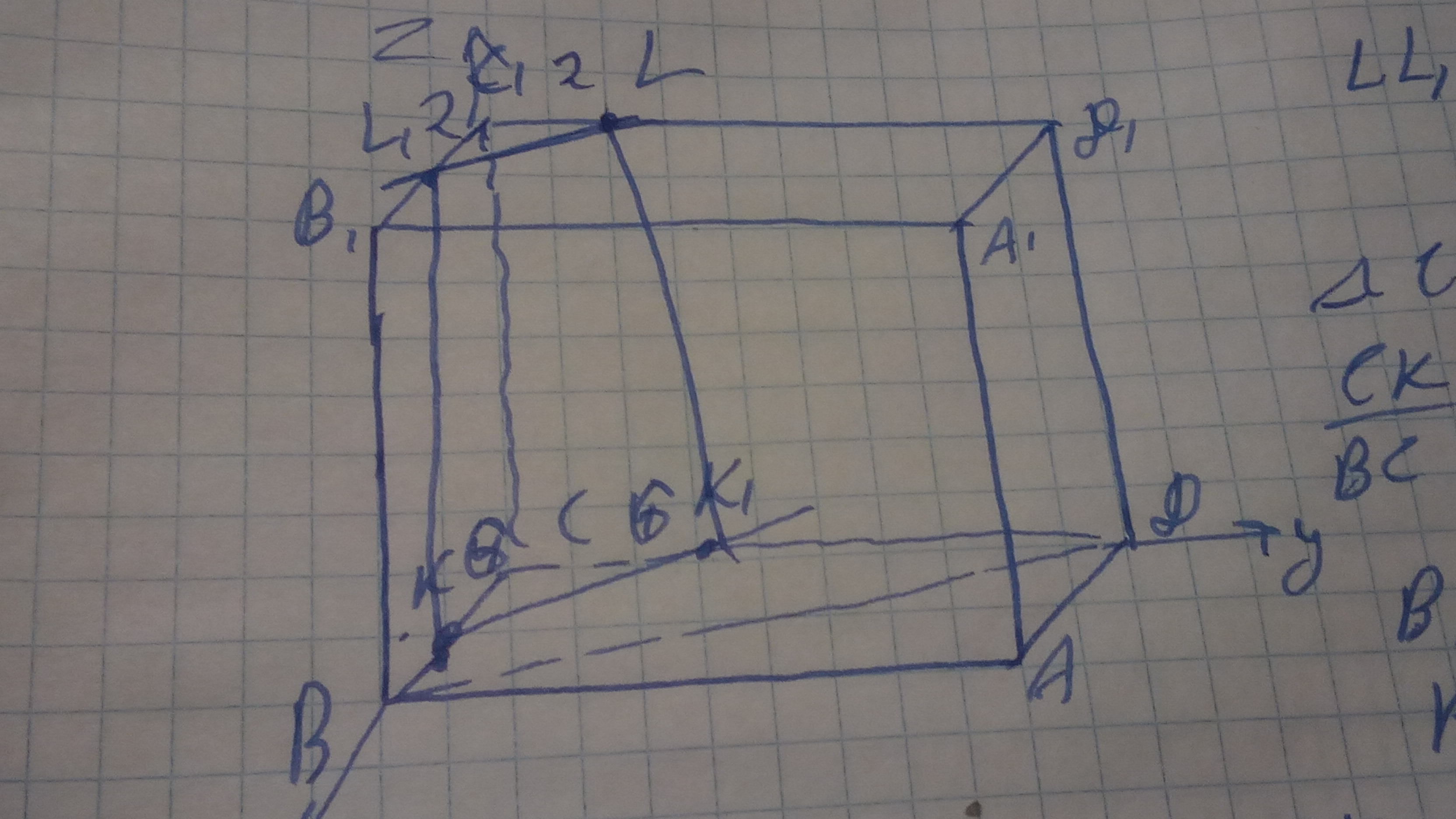
Оси нарисованы .
Координаты точек
В(8;0;0)
К(6;0;0)
L(0;2;4√2)
Третья точка плоскости
К1
КК1 параллельно ВD
K1(0;6;0)

Уравнение плоскости КК1L
ax+by+cz+d=0
Подставляем координаты точек
6а+d=0
2b+4√2c+d=0
6b+d=0
Пусть d= -6 тогда а=1 b=1 c=1/√2
Уравнение
x+y+z/√2-6=0
Нормализованное уравнение плоскости
k=√(1+1+1/2)=√(5/2)

x/k+y/k+z/(√2k)-6/k=0
Подставляем координаты В в нормализованное уравнение
Искомое расстояние равно
8√2/√5-6√2/√5=2√2/√5=2√10/5