Question

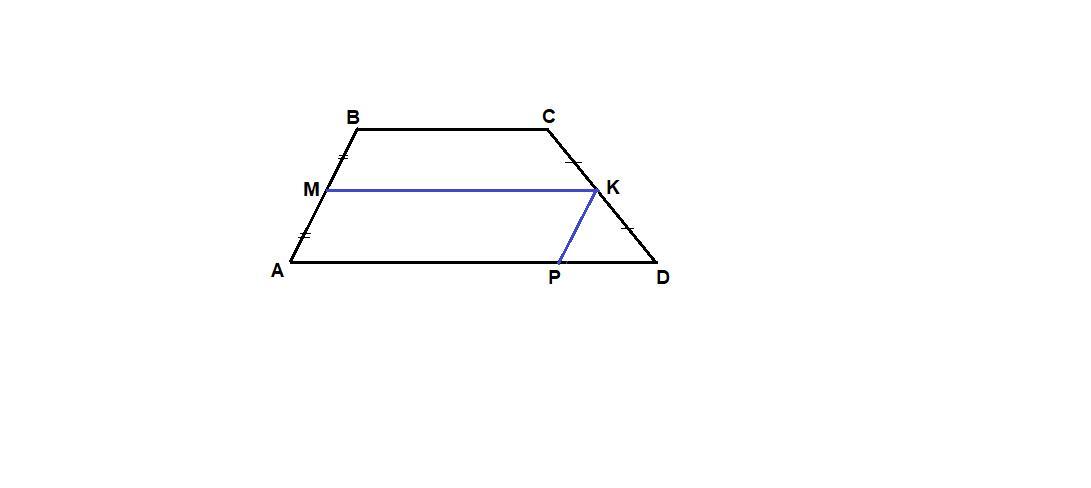
MK-средняя линия трапеции(точки M и К лежат на сторонах AB и CD соответственно) Через точку K проведена прямая параллельна стороне AB и пересекающая сторону ADв точке P
1)докажите что АМКР-параллелограмм
2)найдите периметр параллелограмма АМКР если АВ=4 см ВС=5 см AD=7см ПЛИЗ ПОМОГИТЕ

Answer 1

Ответ:     Р = 16 см

Объяснение:

1) МК║AD как средняя линия трапеции,

КР║АМ по условию, ⇒

АМКР - параллелограмм по определению (противоположные стороны попарно параллельны)

2) АМ = 1/2 АВ = 2 см, так как М - середина АВ,

МК = (AD + BC)/2 = (7 + 5)/2 = 6 см как средняя линия трапеции.

Противоположные стороны параллелограмма равны, тогда периметр:

Pamkp = (AM + MK) · 2 = (2 + 6) · 2  = 16 см