Question

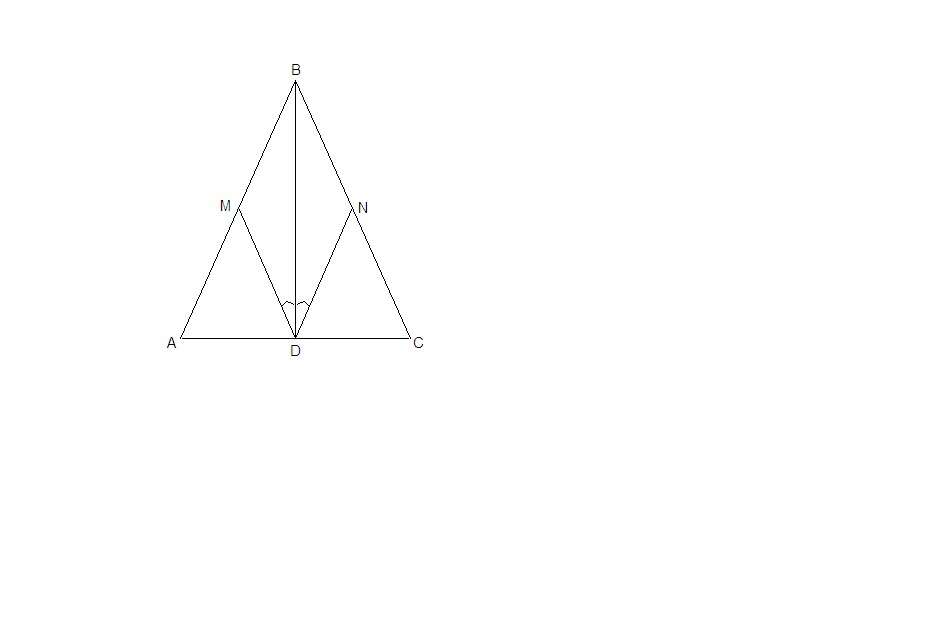
В равнобедренном треугольнике АВС, ВD-высота,проведенная к основанию.Точки M и N принадлежат сторонам AB и BC соответственно.Луч DB-биссектриса угла MDN,Докажите,что AM=NC
Если можно,то и рисунок,пожалуйста,но это не обязательно.

Answer 1

В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой:
∠ABD = ∠CBD,
∠MDB = ∠NDB так как DB - биссектриса угла МDN,
BD - общая сторона для треугольников MDB и NDB, ⇒
ΔMDB = ΔNDB по стороне и двум прилежащим к ней углам.

Из равенства треугольников следует, что
BM = BN.

АМ = АВ - ВМ
CN = CB - BN
AB = CB как стороны равнобедренного треугольника АВС,
значит
AM = CN,