Question

25 Балов! 4 уравнения

Answer 1

Решение задания приложено. В 1 и 2 можно ОДЗ не находить, в сделать проверку корней, Подставив их в уравнение.

Answer 2

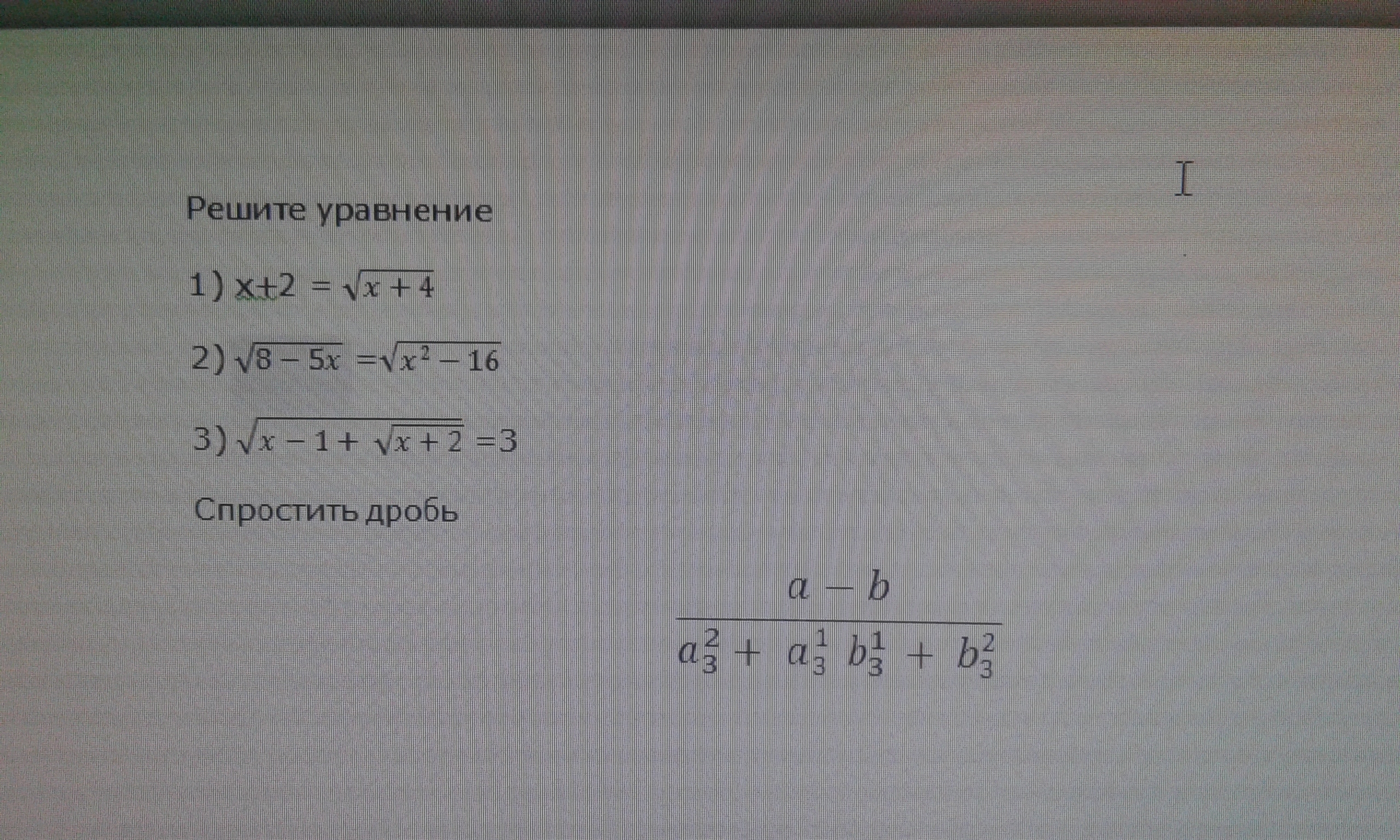
х+2=√(х+4)  ОДЗ х+4≥0  х≥-4 ; х+2>0   x>-2

(х+2)²=√(х+4)²

х²+4х+4= х+4

х²+4х-х+4-4=0

х²+3х=0

х(х+3)=0

х₁=0
 х₂=-3 не подходит под ОДЗ 



------------------------------------------------------------------------------------------

√(8-5х)=√(х²-16)  ОДЗ 8-5х≥0 х≤8/5 ; х²-16≥0  х∈(-∞;-4]∪[4; +∞)

   объединяя обе ОДЗ     х∈(-∞;-4]

√(8-5х)²=√(х²-16)²

8-5х =х²-16

х²+5х-24=0

D=25+96=121  √D=11

x₁=(-5+11)/2=3  не подходит под ОДЗ

x₂=(-5-11)/2=-8  



__________________________________________________________

√(х-1+√(х+2))= 3  ОДЗ  х+2≥0   х ≥-2 ; х-1+√(х+2) ≥0 ⇒ х ≥ 0

√(х-1+√(х+2))²= 3²          

х-1+√(х+2)= 9                   
 
√(х+2))= 9+1-х                  

√(х+2)² = (10-х)²

х+2 =100-20х+х²                

х²-21х+98=0                        

D=441-392 =49   √D=7

x=(21+7)/2=14  √(14-1+√(14+2))= √17≠3 не подходит

x=(21-7)/2=7      √(7-1+√(7+2))=√9 =3

------------------------------------------------------------------------------------------------

a-b                               (a¹/³)³ - (b¹/³)³
-------------------------- = --------------------------------- =
a²/³ +a¹/³b¹/³+b²/³         a²/³ +a¹/³b¹/³+ b²/³

 
(a¹/³ - b¹/³)*( a²/³ +a¹/³b¹/³+ b²/³)
-------------------------------------------- = a¹/³ - b¹/³
 (a²/³ +a¹/³b¹/³+b²/³)

Answer 3

И вот это еще: х-1+√(х+2) ≥0 ⇒ х ≥ 1 - при х=0 получаем: 0-1+1,414 = 0,414

Answer 4

По-моему 0,414 вполне так себе больше нуля, - нет?

Answer 5

"объединяя обе ОДЗ х∈[4; +∞)" - при х=5 под левым корнем отрицательное выражение.

Answer 6

Исправлять будем?

Answer 7

Ошибка при нахождении ОДЗ во 2. Исправьте.