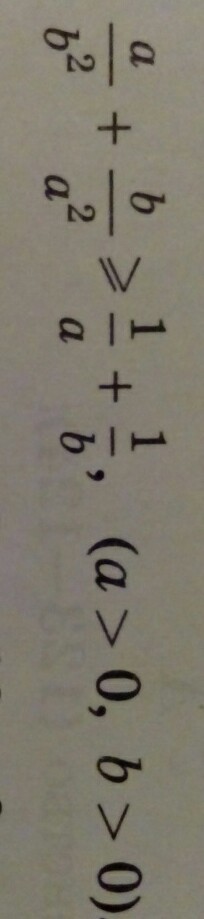Ответы
Ответ дал:
0
a/b^2 + b/a^2 ≥ 1/a + 1/b
(a^3 + b^3)/a^2b^2 ≥ (a + b)/ab
(a^3 + b^3)/ab ≥ a + b
a^3 + b^3 ≥ ab*(a + b)
(a + b)*(a^2 - ab + b^2) ≥ ab*(a + b)
a^2 - ab + b^2 ≥ ab
a^2 - 2ab + b^2 ≥ 0
(a - b)^2 ≥ 0
Неравенство доказано.
Вас заинтересует
3 года назад
3 года назад
10 лет назад