помогите пожалуйста, не могу ничего понять.
Дано: ∆АВС
АК - биссектриса
ВМ - медиана
АК ВМ
АВ = 6 см, ВС = 8 см
Найти: Рabc
Приложения:
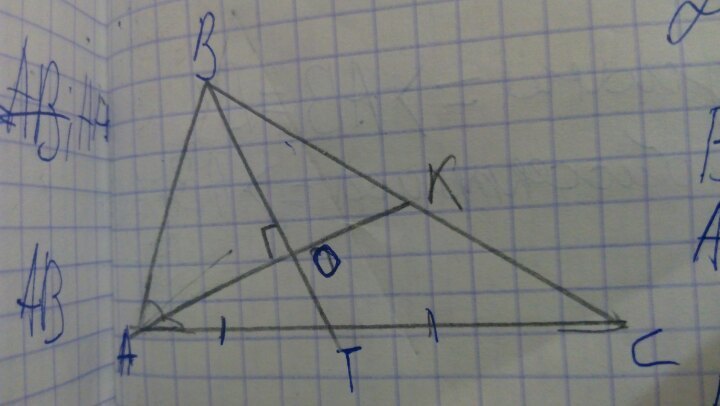
Ответы
Ответ дал:
0
Периметр P=AB+BC+AC. Так как длины сторон AB и BC нам известны, то нужно найти лишь длину стороны AC.
Рассмотрим треугольники AOB и AOM. У них сторона AO - общая, углы OAB и OAT равны, так как AK - биссектриса, а углы AOB и AOT равны как прямые, так как AK⊥BM. Следовательно, треугольники AOB и AOM равны по второму признаку равенства треугольников. Отсюда AM=AB=6 см. А так как BM - медиана, то AC=2*AM=12 см. Тогда P=6+8+12=26 см. Ответ: 26 см.
Рассмотрим треугольники AOB и AOM. У них сторона AO - общая, углы OAB и OAT равны, так как AK - биссектриса, а углы AOB и AOT равны как прямые, так как AK⊥BM. Следовательно, треугольники AOB и AOM равны по второму признаку равенства треугольников. Отсюда AM=AB=6 см. А так как BM - медиана, то AC=2*AM=12 см. Тогда P=6+8+12=26 см. Ответ: 26 см.
Ответ дал:
0
Не угол АОТ, а угол АОМ, конечно.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад