Question

Найти угол при вершине развёртки конуса высотой 8 и радиусом основания 6

Answer 1

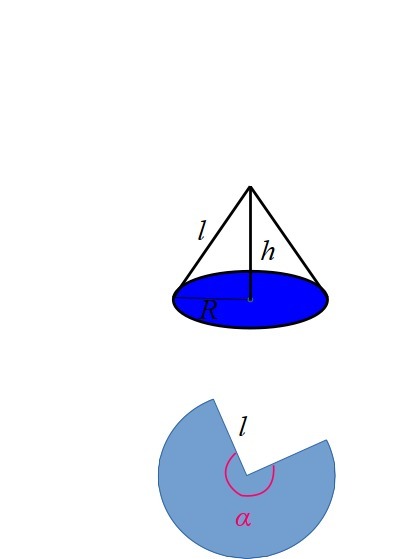
Как из развертки получится конус, думаю понятно. При этом радиус развертки будет образующей конуса l. А длина дуги развертки будет равна длине окружности основания. Находим образующую из теоремы Пифагора.
$l= sqrt{R^2+h^2}= sqrt{6^2+8^2}= sqrt{100}=10$

Известно, что длина дуги равна (радиус дуги)*(ценральный угол)
$L_1= alpha *l$
Отсюда можно выразить угол
$alpha = frac{L_1}{l}$    [1]
А длину дуги мы можем найти, зная что она равна длине окружности основания.
$L_1=2 pi *R$   [2]
Подставляем [2] в [1].
$alpha = frac{2 pi R}{l} = frac{2 pi *6}{10} = frac{6 pi }{5}$
Если в градусах
$alpha = alpha *180/ pi = frac{6 pi*180 }{5* pi } = 36*6=216$

6306354a2a7d7b993e9b954286437969.pdf

Answer 2

да Экспонена ты прав. Спасибо тебе

Answer 3

Правда у меня 216, а не 210 градусов получилось. Проверь расчет. (я тоже проверю) Идею ты понял.

Answer 4

Мож там наоборот h=6 R=8 ?

Answer 5

Хотя и так 210 не будет. Будет даже больше.

Answer 6

Thanks