Разделите параллелограмм на три равных части двумя прямыми, проходящими через вершину. Параллелограмм - произвольный.
Ответы
Ответ дал:
0
Наверное, надо разделить параллелограмм на 3 равных по площади части.
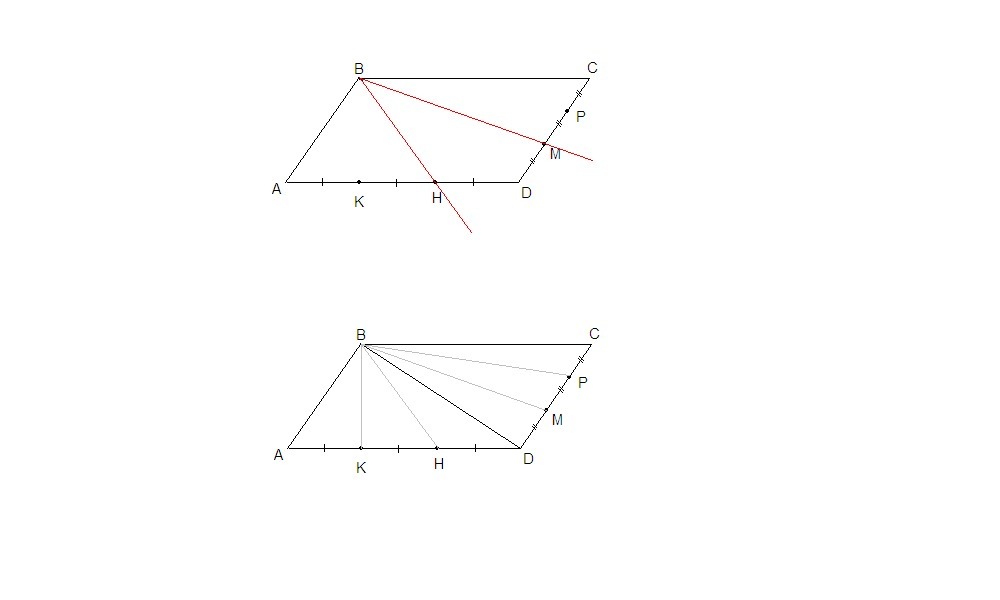
Надо разделить сторону AD на три равных части и сторону CD на три равных части. Затем провести прямые ВН и ВМ.
Площади получившихся частей равны.
Доказательство:
1) Диагональ параллелограмма делит его на два равных треугольника, значит и площади их равны:
Sabd = Scbd.
2) Треугольники, имеющие общую высоту и равные основания, имеют равные площади. Поэтому
Sbak = Sbkh = Sbhd = 1/3 · Sabd
и
Sbdm = Sbmp = Sbpc = 1/3 · Scbd
То есть получилось шесть треугольников одинаковой площади.
Осталось объединить их по 2.
Надо разделить сторону AD на три равных части и сторону CD на три равных части. Затем провести прямые ВН и ВМ.
Площади получившихся частей равны.
Доказательство:
1) Диагональ параллелограмма делит его на два равных треугольника, значит и площади их равны:
Sabd = Scbd.
2) Треугольники, имеющие общую высоту и равные основания, имеют равные площади. Поэтому
Sbak = Sbkh = Sbhd = 1/3 · Sabd
и
Sbdm = Sbmp = Sbpc = 1/3 · Scbd
То есть получилось шесть треугольников одинаковой площади.
Осталось объединить их по 2.
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
10 лет назад