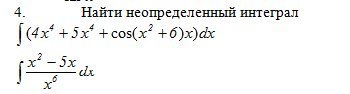Ответы
Ответ дал:
0
На фото задания 40б нет, поэтому решаю всё, что есть:
А.
Приведём подобные разобьём интеграл суммы на сумму интегралов:

Первый интеграл по правилам интегрирования степенной функции:

Для взятия второго интеграла приведём его к виду, когда дифференциал совпадает аргументом косинуса, чтобы воспользоваться табличным интегралом от косинуса.
Косинус умножается на x, если икс загнать под дифференциал, то получится: . А константа приплюсовывается без проблем, т.к. её производная равна нулю:
. А константа приплюсовывается без проблем, т.к. её производная равна нулю:

Итак, находим второй интеграл:

А теперь суммируем оба решения:

Б.
Для вычисления интеграла находим частное, появится простая степенная функция с отрицательными степенями:

А.
Приведём подобные разобьём интеграл суммы на сумму интегралов:
Первый интеграл по правилам интегрирования степенной функции:
Для взятия второго интеграла приведём его к виду, когда дифференциал совпадает аргументом косинуса, чтобы воспользоваться табличным интегралом от косинуса.
Косинус умножается на x, если икс загнать под дифференциал, то получится:
Итак, находим второй интеграл:
А теперь суммируем оба решения:
Б.
Для вычисления интеграла находим частное, появится простая степенная функция с отрицательными степенями:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад