Question

стороны основания правильной треугольной пирамиды равны 14 ,а боковые ребра равны 25 .найдите площадь боковой поверхности этой пирамиды

Answer 1

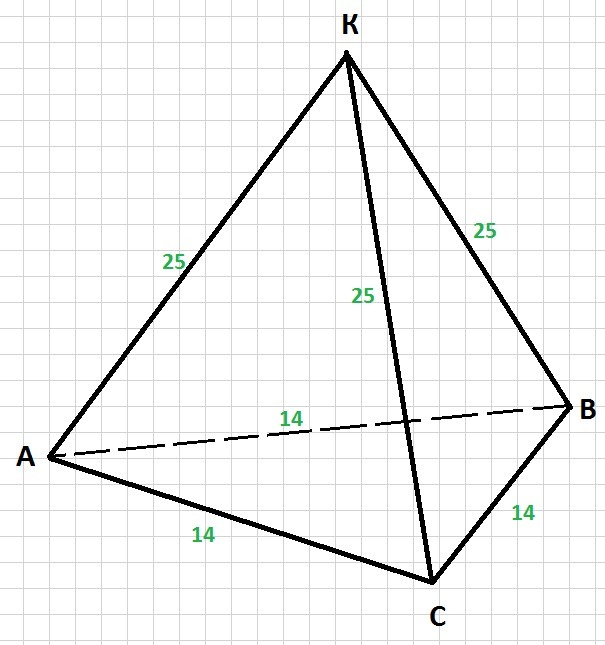
Пирамида правильная, значит боковыми гранями являются три равных между собой равнобедренных треугольника (смотри рисунок)

По формуле Герона найдем площадь одной боковой грани и полученный результат умножим на 3. Это и будет площадь боковой поверхности пирамиды.

$S=sqrt{p(p-a)(p-b)(p-c)}$, где р - полупериметр, а, b, с - стороны треугольника.

а=14

b=с=25

$p=frac{a+b+c}{2} =frac{14+25+25}{2}=32$

$S=sqrt{32(32-14)(32-25)(32-25)} =sqrt{32*18*7*7}= sqrt{2*16*2*9*7*7}=2*7*4*3=168$ - площадь одной боковой грани пирамиды.

S бок. = 3*168 = 504 - площадь боковой поверхности пирамиды.