Пожалуйста) Вокруг конуса с радиусом основания 10 см, высота 24 см. Описаны правильно треугольную пирамиду. Найдите площадь боковой грани пирамиды.
Ответы
Ответ дал:
0
Основание пирамиды - описанный вокруг основания конуса равносторонний треугольник. Центр вписанной в треугольник окружности лежит в точке пересечения биссектрис. Для правильного треугольника эта точка является и точкой пересечения медиан и высот.
Радиус окружности, вписанной в правильный треугольник, равен 1/3 его высоты.
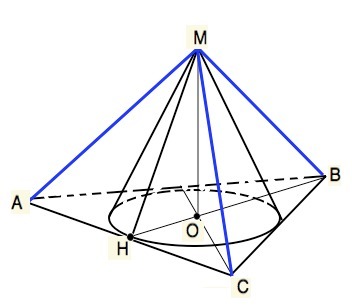
Обозначим основание пирамиды АВС, вершину М ( совпадает с вершиной конуса).
Высота основания ВН=3r=30
АВ=ВН:sin60°=30:√3/2=60•2/√3=20√3
Формула площади боковой поверхности правильной пирамиды
S=p•h:2, т.е. произведение полупериметра на пофему.
По т.Пифагора апофема
МН=√(МО²+ОН²)=√(576+100)=26
р=0,5•3•20√3 =30√3
S=26•30√3=780√3
Приложения:
Вас заинтересует
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад