Question

Решите задачу
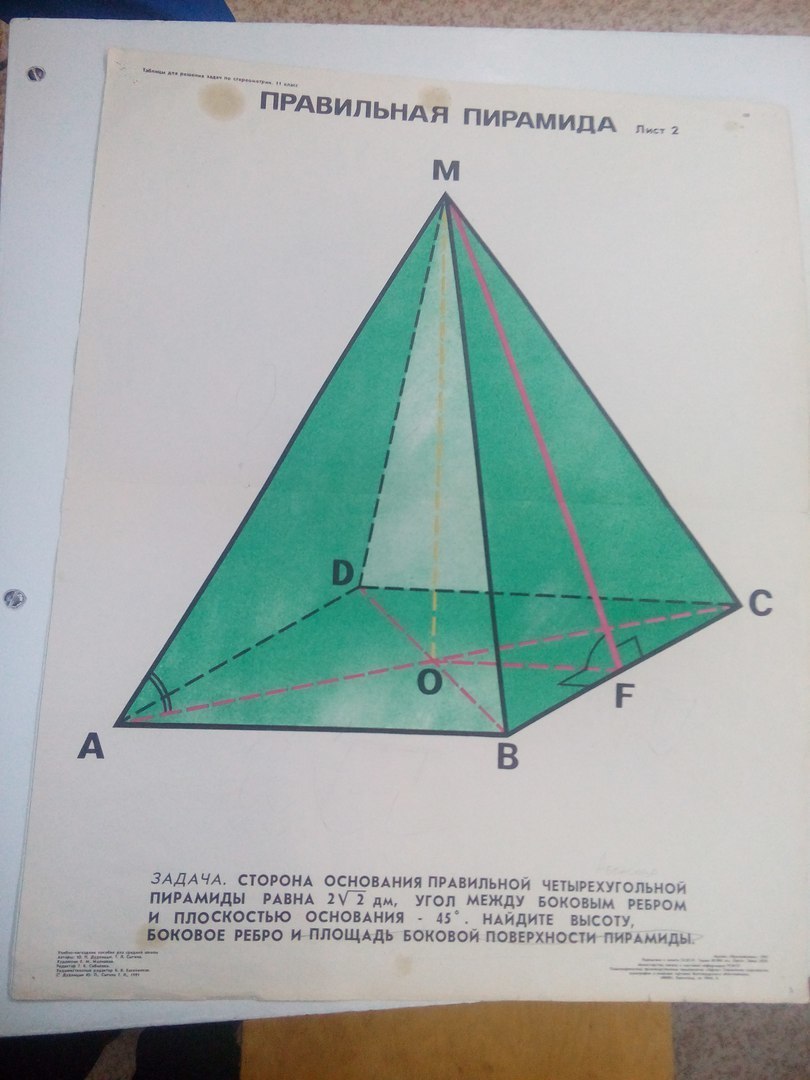
Сторона основания правильной четырёхугольной пирамиды равна 2 корня 2 дм, угол между боковым рёбром и плоскостью основания - 45 градусов. найдите высоту, боковое ребро и площадь боковой поверхности пирамиды.

Answer 1

В основании - квадрат со стороной 2$sqrt{2}$ дм.
Диагональ квадрата   AC = AB * $sqrt{2}$ =  2$sqrt{2}$ * $sqrt{2}$  = 4 дм.
AO = AC / 2 = 2 дм
ΔAMO - прямоугольный равнобедренный, высота OM = AO = 2 дм  
ΔAMO = ΔAOB  по общему катету АО и углу 45°,
       поэтому боковое ребро AM = AB = 2$sqrt{2}$ дм.

ΔAMB - равносторонний.
Площадь ΔAMВ = АВ^2 * $sqrt{3}$ / 4  =
                            = (2$sqrt{2}$)^2 * $sqrt{3}$ /4 =
                            =  2$sqrt{3}$

Площадь боковой поверхности = 4 * площадь ΔAMВ  =  8$sqrt{3}$ дм^2

Ответ:  Высота 2 дм, боковое ребро 2$sqrt{2}$ дм, 
             Площадь боковой поверхности =  8$sqrt{3}$ дм^2