1)Вычислить объём тела,полученного вращением фигуры ф вокруг указанной оси.
ф:p=2(1+cos ф), полярная ось
2)вычислить площадь поверхности,образованной вращением дуги кривой L вокруг указанной оси.
L:x=t-sin t,y=1-cos t(0<=t<=2п)
Ответы
Ответ дал:
0
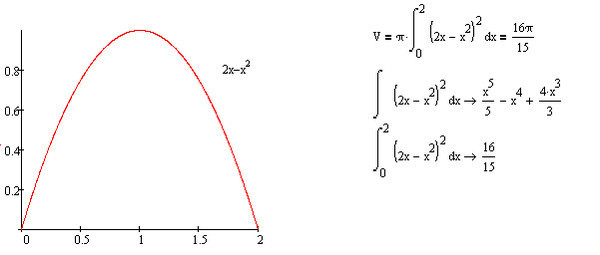
1)вот
2)Площадь поверхности вращения вычисляется по известной
формуле:
S=2pi*int [0;2pi] y(t)ds, где ds=koren(x'^2+y'^2)dt=dt,
Итак, S=2pi*int[0;2pi](3+sin t)dt=12(pi)^2.
Примечание: эта поверхность - тор ("бублик").
2)Площадь поверхности вращения вычисляется по известной
формуле:
S=2pi*int [0;2pi] y(t)ds, где ds=koren(x'^2+y'^2)dt=dt,
Итак, S=2pi*int[0;2pi](3+sin t)dt=12(pi)^2.
Примечание: эта поверхность - тор ("бублик").
Приложения:
Вас заинтересует
2 года назад
2 года назад
9 лет назад
10 лет назад