Question

помогите по геометрии ,дам 10б

Answer 1

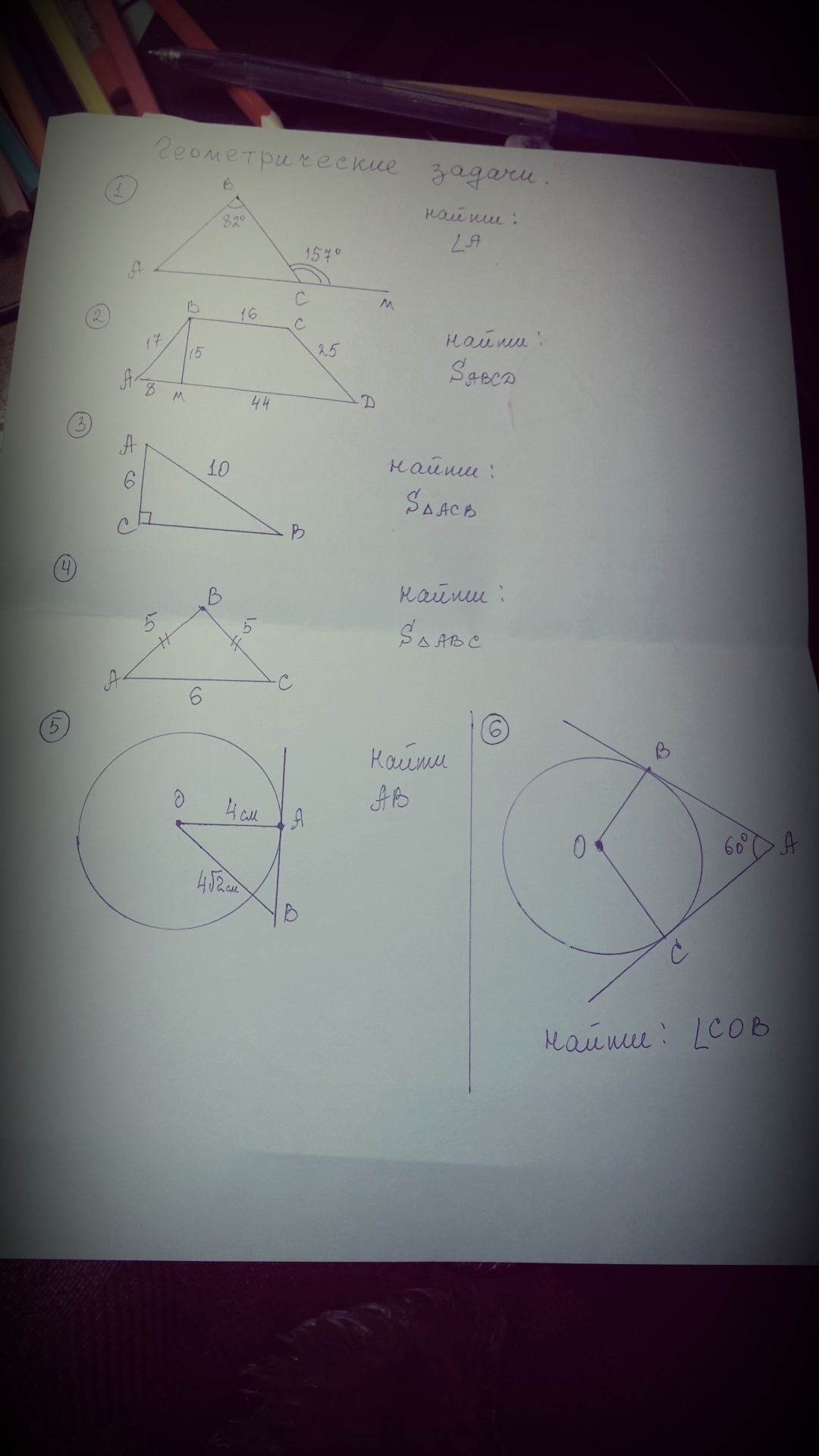
Номер один

Решение:
∠АСВ и ∠ВСМ — смежные ⇒ ∠АСВ = 180° - ∠ВСМ = 180° - 157° = 23°.
По теореме о сумме углов треугольника:
∠А = 360° - ∠АВС - ∠ВСА = 180° - 82° - 23° = 75°.
Ответ: 75.

Номер два

Решение:
S$__{ABCD}$ = $frac{1}{2}$(BC + (AМ + МD)) × ВМ = $frac{1}{2}$(16 + 52) × 15 = 34 × 15 = 510
Ответ: 510.

Номер три:

S$__{ABC}$ = $frac{1}{2}$АС × СВ.
По теореме Пифагора:
СВ² = АВ² - АС² = 100 - 36 = 64
СВ = $sqrt{64}$ = 8
S$__{ABC}$ = $frac{1}{2}$ × 6 × 8 = 24
Ответ: 24.

Номер четыре:

Решение:
Проведём высоту ВН. Так как АВ = АС (треугольник АВС — равнобедренный), то ВН также является медианой ⇒ АН = $frac{1}{2}$АС = 3.
По теореме Пифагора:
ВН² = АВ² - АН² = 5² - 3² = 25 - 9 = 16
ВН = $sqrt{16}$ = 4
S$__{ABC}$ = $frac{1}{2}$ВН × АС = $frac{1}{2}$ × 4 × 6 = 12
Ответ: 12.

Номер пять

Решение:
Так как касательная к окружности перпендикулярна к радиусу, проведённому в точку касания, то ∠ОАВ = 90°.
По теореме Пифагора:
АВ² = ОВ² - ОА² = (4$sqrt{2}$)² - 4² = 32 - 16 = 16
АВ = $sqrt{16}$ = 4.
Ответ: 4.

Номер шесть

Решение: 
Проведём хорду ВС. Рассмотрим треугольник АВС:
АВ = АС как касательные, проведённые из одной точки ⇒ треугольник АВС — равнобедренный. По теореме о сумме углов треугольника: ∠АВС + ∠АСВ = 180° - ∠ВАС = 180° - 60° = 120°. ∠АВС = ∠АСВ = $frac{1}{2}$ × 120° = 60°.
Так как касательная к окружности перпендикулярна к радиусу, проведённому в точку касания, то ∠ОВС = 90° - ∠АВС = 90° - 60° = 30°. ОВ = ОС как радиусы ⇒ треугольник ОВС — равнобедренный и ∠ОСВ = ∠ОВС = 30°. По теореме о сумме углов треугольника: ∠СОВ = 180° - ∠ОСВ - ∠ОВС = 180° - 30° - 30° = 120°.
Ответ: 120.