Question

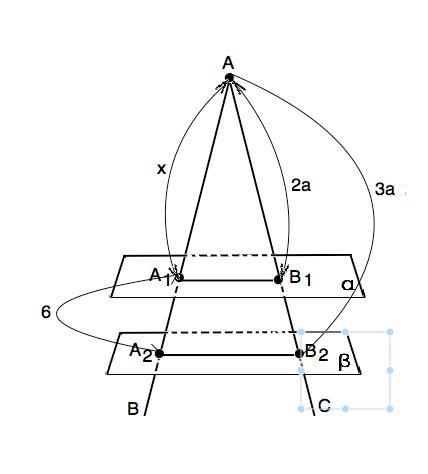
Параллельные плоскости альфа и бета пересекают сторону АВ угла ВАС соответственно в точках А1 и А2, а сторону АС этого угла в В1 и В2. Найти АА1 если А1А2=6, АВ2:АВ1=3:2 ? помогите срочно нужно

Answer 1

Ответ: 12 (ед. длины)

Объяснение:

   Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. ⇒ А1В1║А2В2

Стороны угла – секущие при параллельных А1В1 и А2В2, ⇒ соответственные углы при их пересечении равны.

Треугольники АА1В1 и АА2В2 подобны по трем углам.

  Примем АА1=х   Тогда  АА2=х+6 .

Из подобия треугольников АА2 и АА1 следует отношение: 

(х+6):х=3:2 

3х=2х+12 

х=12 

АА1=12 (ед. длины)