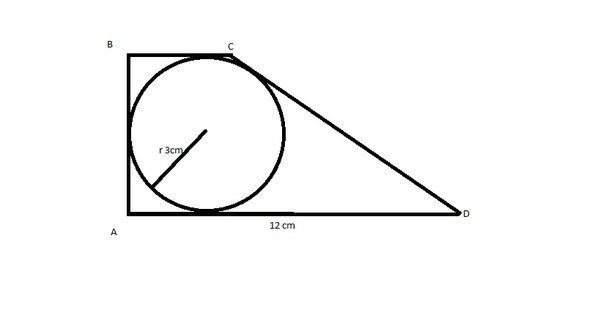
Дана прямоугольная трапеция, большее основание которого равно 12 см, а радиус вписанной в неё окружности - 3 см. Найдите площадь трапеции.
Ответы
Ответ дал:
0
Обозначим точку касания окружности нижнего основания заданной трапеции АВСД буквой К, а верхнего основания буквой М
Высота трапеции (она прямоугольная) равна 2r = 2*3 = 6 см.
Часть нижнего основания КД = 12 - 3 = 9 см.
Угол α = МОС равен углу ОДК как взаимно перпендикулярные.
tg α = 3/9 = 1/3.
МС = r*tg α = 3*(1/3) = 1 см.
Отсюда верхнее основание равно 3 + 1 = 4 см.
Тогда площадь трапеции S =6*((4+12)/2) = 6*8 = 48 cм².
Высота трапеции (она прямоугольная) равна 2r = 2*3 = 6 см.
Часть нижнего основания КД = 12 - 3 = 9 см.
Угол α = МОС равен углу ОДК как взаимно перпендикулярные.
tg α = 3/9 = 1/3.
МС = r*tg α = 3*(1/3) = 1 см.
Отсюда верхнее основание равно 3 + 1 = 4 см.
Тогда площадь трапеции S =6*((4+12)/2) = 6*8 = 48 cм².
Приложения:
Ответ дал:
0
Можно рисунок?
Ответ дал:
0
Вот.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад