В треугольнике ABC, AB=10 см, BC=9 см, AC= 17 см. В каком отношении центр окружности, вписанной в треугольник, делит его биссектрису AM?
Ответы
Ответ дал:
0
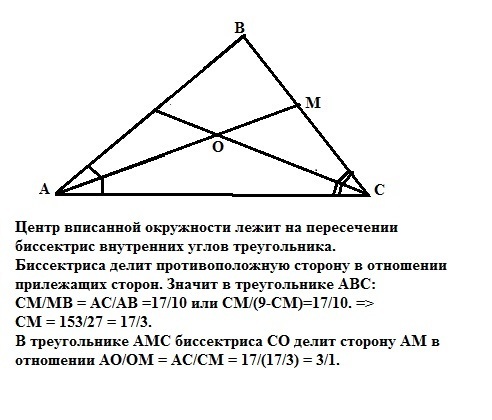
Центр вписанной окружности лежит на пересечении биссектрис внутренних углов треугольника.
Биссектриса делит противоположную сторону в отношении прилежащих сторон. Значит в треугольнике АВС:
СМ/МВ = АС/АВ =17/10 или СМ/(9-СМ)=17/10. => СМ = 153/27 = 17/3.
В треугольнике АМС биссектриса СО делит сторону АМ в отношении АО/ОМ = АС/СМ = 17/(17/3) = 3/1.
Ответ: АО/ОМ = 3/1.
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад