Ответы
Ответ дал:
0
1.1.

1.2.


1.3. Интегрирование по частям:



2.1.

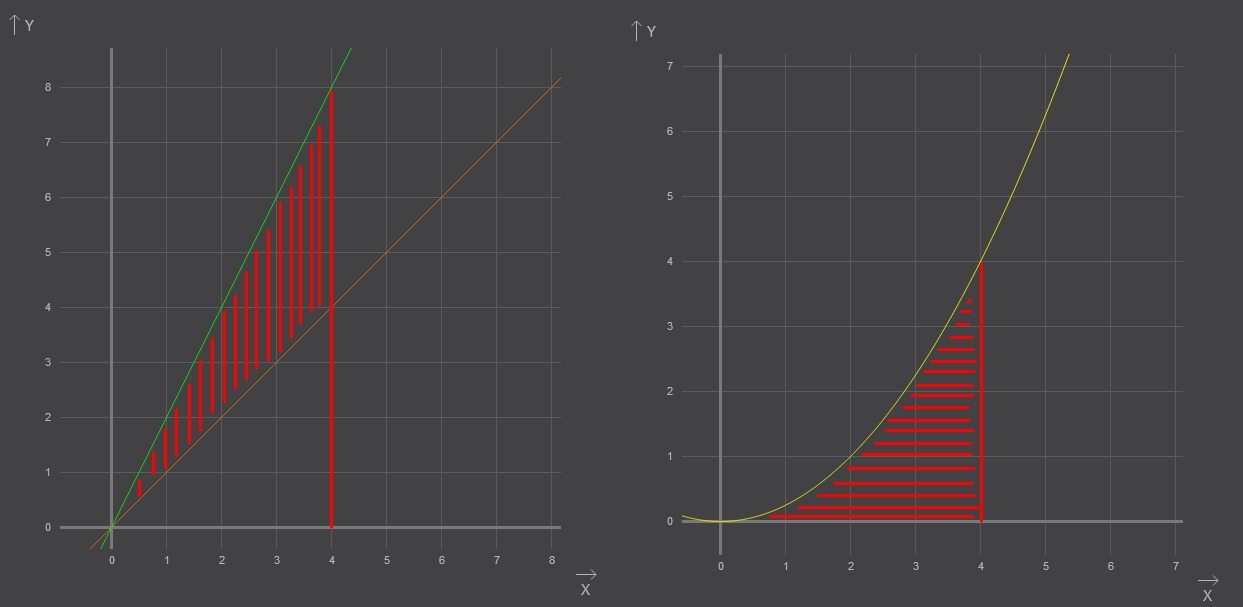
Найдем второй предел интегрирования как абсциссу точки пересечения графиков:


2.2.
Один предел интегрирования x=4, находим второй:


1.2.
1.3. Интегрирование по частям:
2.1.
Найдем второй предел интегрирования как абсциссу точки пересечения графиков:
2.2.
Один предел интегрирования x=4, находим второй:
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад
