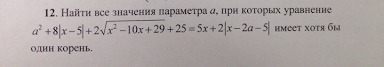Ответы
Ответ дал:
0
Сделаем замену t = x - 5, тогда x = t + 5. Очевидно, у исходного уравнения и у уравнения относительно t должно быть одинаковое количество корней.

Раскроем один из модулей:


Рассмотрим правую часть уравнения из первой системы. В левой части стоит квадрат числа, так что для того, чтобы уравнение имело корни, правая часть должны быть неотрицательна.
Если t < 0, то

Если t > 0, то

Итак, при t не равных нулю правая часть отрицательна, так что корней у уравнения нет. Значит, корни могут быть только при t = 0.
Аналогично, и уравнение из второй системы имеет решения, только если t = 0. Поэтому если совокупность и имеет решение, то оно нулевое. Найдём, при каких a решением совокупности будет t = 0.

Ответ.
Раскроем один из модулей:
Рассмотрим правую часть уравнения из первой системы. В левой части стоит квадрат числа, так что для того, чтобы уравнение имело корни, правая часть должны быть неотрицательна.
Если t < 0, то
Если t > 0, то
Итак, при t не равных нулю правая часть отрицательна, так что корней у уравнения нет. Значит, корни могут быть только при t = 0.
Аналогично, и уравнение из второй системы имеет решения, только если t = 0. Поэтому если совокупность и имеет решение, то оно нулевое. Найдём, при каких a решением совокупности будет t = 0.
Ответ.
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад