Question

Найдите промежутки возрастания и убывания функции,точки экстремума

у=$x^{3}$-12х+3

Очень прошу,помогите

Answer 1

$y=x^3-12x+3\y'=3x^2-12\3x^2-12=0\x=+-2$
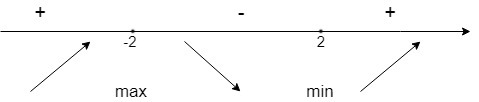
Отмечаем получившиеся точки на числовой прямой. Для определения знака производной достаточно взять по точке на каждом из интервалов:
 (-∞;-2] ∪ [-2;2] ∪ [2;∞].
y'(3) для промежутка [2;∞], подставляем в производную - y'. 
y'(3) > 0, ⇒ крайний правый промежуток имеет знак " + ".
y'(1) < 0, ⇒ на отрезке [-2;2] знак " - ".
Аналогично для двух других...

На промежутках где производная положительная - функция возрастает; отрицательная - убывает.
Возрастает: [ - ∞;-2] ∪ [2;∞]
Убывает: [-2;2]