Question

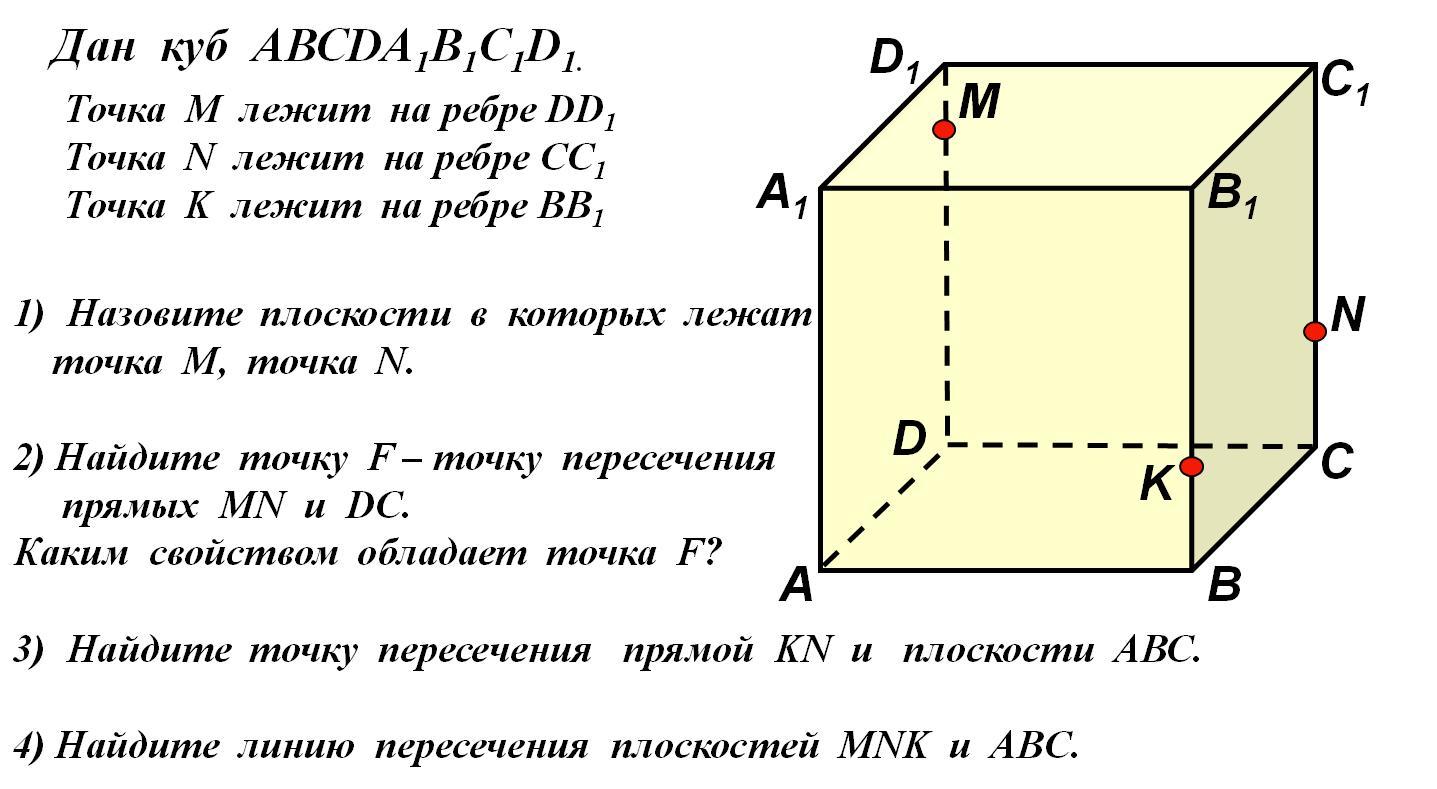
Дан куб АВСDA1B1C1D1. Точка М лежит на ребре DD1. Точка N лежит на ребре CC1. Точка K лежит на ребре BB1.

а) Назовите плоскости в которых лежат точка М, точка N.
б) Найдите точку F – точку пересечения прямых MN и DС.
в) Найдите точку пересечения прямой KN и плоскости АВС.

Помогииите пожалуйста

Answer 1

Полное условие смотри в 1 приложении.

Чертежи к решению смотри во втором приложении.

Если точка принадлежит прямой, которая лежит в плоскости, то точка принадлежит этой плоскости.

1)

M ∈ DD₁ ⊂ (ADD₁),(CDD₁)

Поэтому M ∈ (ADD₁),(CDD₁)

N ∈ CC₁ ⊂ (DCC₁),(BCC₁)

Поэтому N ∈ (DCC₁),(BCC₁)

2)

Продлим прямые MN и DC, лежащие в одной плоскости DCC₁.

MN ∩ DC = F.

F ∈ MN ⊂ (DCC₁), поэтому F ∈ (DCC₁);

F ∈ DC ⊂ (DCC₁), поэтому F ∈ (ADC).

3)

Продлим прямые KN и CB, лежащие в одной плоскости BCC₁. Точку пересечения обозначим буквой P.

P ∈ CB ⊂ (ABC), поэтому P ∈ (ABC), так же P ∈ KN.

Получаем, что KN ∩ (ABC) = P.

4)

P ∈ (ABC);

F ∈ DC ⊂ (ABC), поэтому F ∈ (ABC);

То есть PF ⊂ (ABC).

P ∈ KN ⊂ (MNK), поэтому P ∈ (MNK);

F ∈ MN ⊂ (MNK), поэтому F ∈ (MNK);

То есть PF ⊂ (MNK).

PF ⊂ (ABC),(MNK)  поэтому (ABC) ∩ (MNK) = PF.