Решите пожалуйста.
Под буквой "б" объясните подробно...
А) 5cosx + 4/ 4tgx -3 =0
Б) [-4п; -5п/2 ]
Ответы
Ответ дал:
0
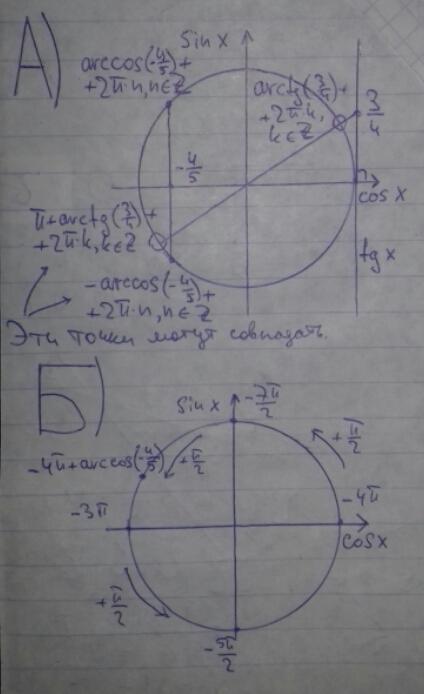
А)
Если , то для х ∈ 3ч. :
Значит на тригонометрической окружности точки и
совпадают, поэтому решением системы будет
Б)
На промежутке [0;2π] корнем системы будет:
Значит на промежутке [-4π;-2π] корень будет:
Заданный в условии промежуток не ограничивает корень системы на промежутке [-4π;-2π].
Ответ: А)
Б)
Приложения:
Вас заинтересует
2 года назад
3 года назад
9 лет назад
10 лет назад