составить уравнение линии, для каждой точки которой ее расстояние до точки A(x1; y1) равно расстоянию до прямой y = b. Полученное уравнение привести к простейшему виду и построить кривую.
A (2;1), b=-1
Ответы
Ответ дал:
0
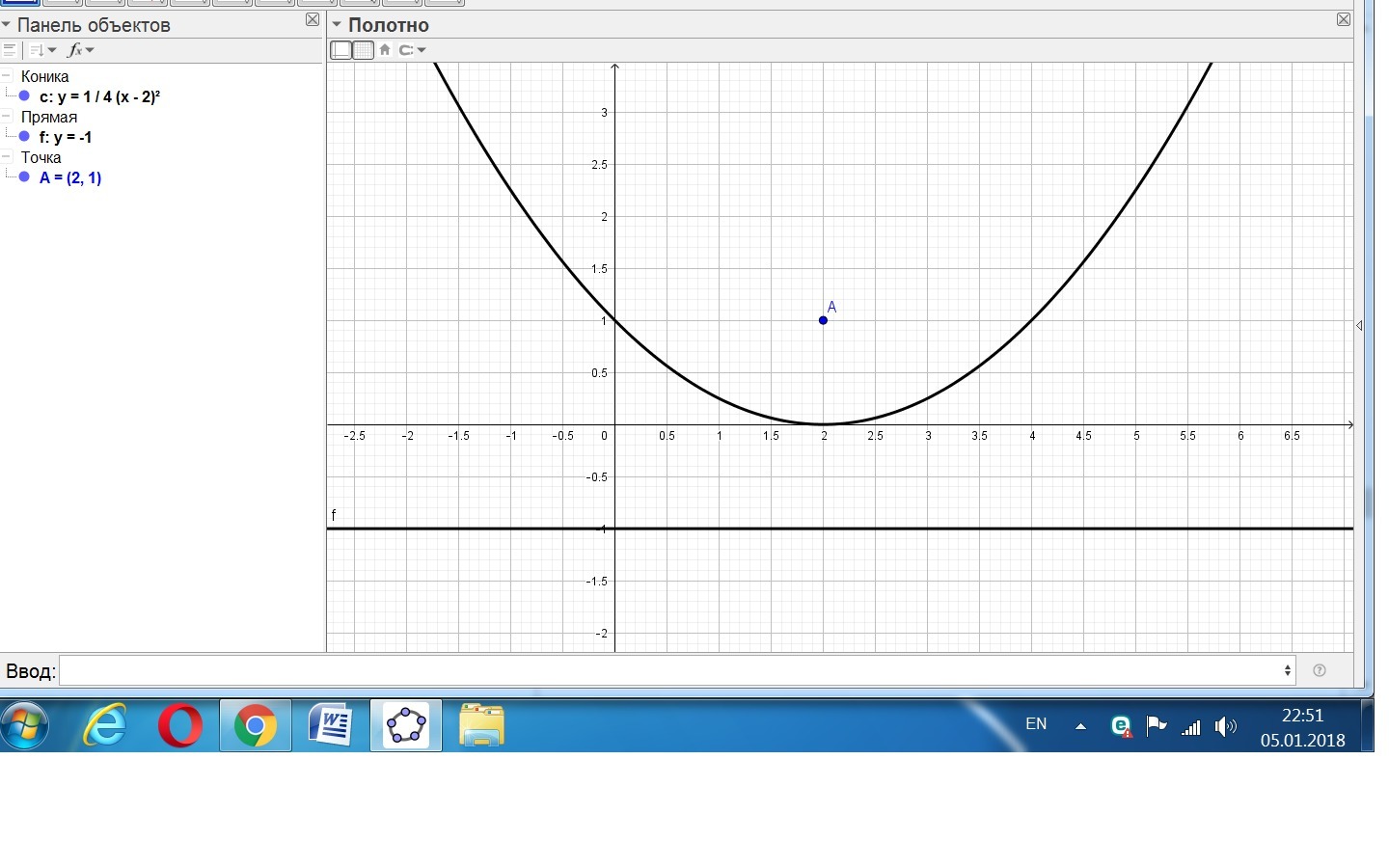
Пусть М(х;у) — текущая точка искомой кривой. Опустим из точки М перпендикуляр МВ на прямую у = -1 (см. приложение). Тогда В (х; -1).
Так как МА=МВ, то
Возведём обе части в квадрат.

Раскроем скобки с переменной у:

Получаем уравнение параболы:

Так как МА=МВ, то
Возведём обе части в квадрат.
Раскроем скобки с переменной у:
Получаем уравнение параболы:
Полученное уравнение определяет параболу с вершиной в точке О*(2; 0). Для приведения уравнения параболы к простейшему (каноническому) виду положим x – 2 = X*, y = Y*.
Тогда в системе координат Х*0*У* уравнение параболы принимает следующий вид: У*= (1/4)(Х*)².
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад