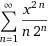Ответы
Ответ дал:
0
Найдем радиус сходимости по признаку Даламбера

Областью сходимости степенного ряда является интервал (-R;R). Значит ряд является сходящимся при всех x, принадлежащих интервалу (-2;2).
Исследуем теперь сходимость ряда на концах этого интервала.
Положим тогда получим сумму ряда
тогда получим сумму ряда  и по признаку Даламбера этот ряд расходится, значит х=±2 является точкой расходимости.
и по признаку Даламбера этот ряд расходится, значит х=±2 является точкой расходимости.
Ответ: степенной ряд является сходящимся при x ∈ (-2;2)
Областью сходимости степенного ряда является интервал (-R;R). Значит ряд является сходящимся при всех x, принадлежащих интервалу (-2;2).
Исследуем теперь сходимость ряда на концах этого интервала.
Положим
Ответ: степенной ряд является сходящимся при x ∈ (-2;2)
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад