Question

помогите пожалуйста! С чертежом...

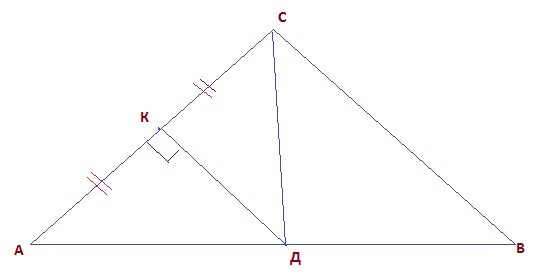
Серединный перпендикуляр к стороне АС в треугольнике АВС пересекает сторону АВ в точке Д. Точка Д соединена отрезком с вершиной С. Докажите, что треугольник АДС равнобедренный.

Answer 1

В ΔАКД и ΔКДС АК=КС, ∠АКД=∠СКД, так как КД⊥АС, по условию, значит
ΔАКД=ΔКДС по первому признаку. В равных треугольниках против равных углов лежат равные стороны⇒АД=ДС и ΔАДС-равнобедренный, что и требовалось доказать.
Другое решение:
ДК- медиана и высота ΔАСД, а это является свойством  равнобедренных треугольников. В равнобедренном треугольнике: высота и медиана, исходящие из угла, образованного равными сторонами, один и тот же отрезок⇒АД=ДС и ΔАДС-равнобедренный.

Answer 2

Спасибоньки! :3