Question

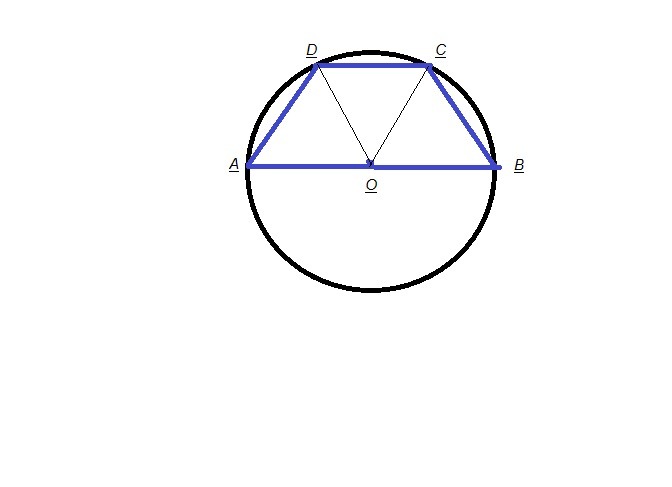
Вершины четырехугольника ABCD лежат на окружности с центром О,AB-диаметр и AD=CD=CB. Докажите,что треугольники AOD,DOC,COB равны.Найдите,чему равен угол DOC.Пеесекаются ли прямые AB и CD,если угол ODA=60 градусов

Answer 1

Так как АВ - диаметр, то точки С и D  четырёхугольника АВСD могут лежать только по одну сторону от диаметра.
  Если AD=CD=CB , то дуга АDCB  делиться на 3 равные дуги AD=DC=CB.
Тогда  ∠AOD=∠DOC=∠COB =180°:3=60°. 
  Так как радиус R=OA=OD=OC=OB, то по 1 признаку равенства треугольников получаем  ΔAOD=ΔDOC=ΔCOB . Эти треугольники являются ещё и равносторонними ( т.к. они равнобедренные с углом
в 60° ).
Поэтому  ∠ODA=60°.
АВ и CD не пересекаются, они параллельны.