Помогите с 3 заданиями. Даю Cамое большое кол-во баллов. Срочо. Плиз
1. Найти область определения функции
а) Y =√(2x - 5) б) Y = 6/(x - 1)
в) y = √( (x - 5) / (2x + 3) ) г) Y = 2x / (х^2 - 5x + 6)
2. Исследовать функции на четность, нечетность
а) Y = x^3 / (х^2+ 1) б) Y = x^4 – 2x^2 + 3 в) Y = x^3 - 5x + 1
3. исследовать функцию на возрастание и убывание
а) Y = 2x б) Y = -3x + 2 в) Y = 2x^2 + 5
Ответы
Ответ дал:
0
1. а) Выражение под корнем всегда неотрицательно. Тогда D(y): 
б) Выражение в знаменателе не равно нулю. Тогда D(y):
в) Выражение под корнем всегда неотрицательно. Тогда D(y):
г) Выражение в знаменателе не равно нулю. Тогда D(y): (решение квадратного уравнение расписывать не буду, это алгоритм)
2. а) D(y) = (знаменатель в ноль не обращается) - симметричное множество.
(знаменатель в ноль не обращается) - симметричное множество.

Функция нечётная
б) D(y) = (ограничений нет) - симметричное множество.
(ограничений нет) - симметричное множество.

Функция чётная
в) D(y) = (ограничений нет) - симметричное множество.
(ограничений нет) - симметричное множество.

Функция общего вида
3. а) Это прямая, k > 0, значит, функция всегда возрастает
б) Это прямая, k < 0, значит, функция всегда убывает
в) Это парабола, a > 0 (ветви направлены вверх), вершина имеет координату 0 по x (-b/2a = -0/4 = 0), значит, на (-∞; 0] убывает, на [0; +∞) возрастает
б) Выражение в знаменателе не равно нулю. Тогда D(y):
в) Выражение под корнем всегда неотрицательно. Тогда D(y):
г) Выражение в знаменателе не равно нулю. Тогда D(y): (решение квадратного уравнение расписывать не буду, это алгоритм)
2. а) D(y) =
Функция нечётная
б) D(y) =
Функция чётная
в) D(y) =
Функция общего вида
3. а) Это прямая, k > 0, значит, функция всегда возрастает
б) Это прямая, k < 0, значит, функция всегда убывает
в) Это парабола, a > 0 (ветви направлены вверх), вершина имеет координату 0 по x (-b/2a = -0/4 = 0), значит, на (-∞; 0] убывает, на [0; +∞) возрастает
Приложения:
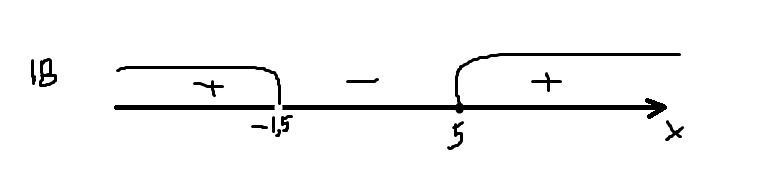
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад