Высота конуса 8мм, образующая боковой поверхности 10 мм. Найдите: 1. Радиус вписанного шара; 2. Длинну линии касания
Ответы
Ответ дал:
0
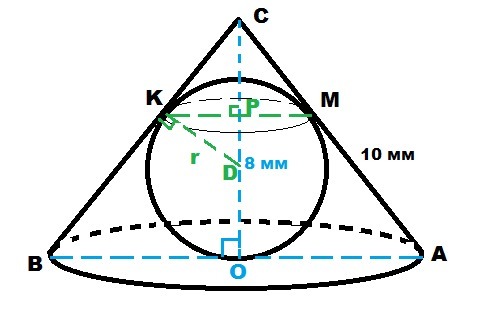
Дано: в конус вписан шар; h = OC = 8 мм; AC = 10 мм
Найти: r - ?; длину линии касания
Для решения нужно провести сечение конуса по диаметру основания, в сечении будет равнобедренный ΔBCA
ΔAOC - прямоугольный. По теореме Пифагора
OA² = AC² - h² = 100 - 64 = 36 = 6²
OA = 6 мм
ΔBCA равнобедренный ⇒ BA = 2·OA= 2·6 = 12 мм
Площадь треугольника

Площадь треугольника через радиус вписанной окружности

16r = 48 ⇒ r = 3 мм
Длина касания - это длина окружности
с центром в точке P и радиусом KP
ΔDKC - прямоугольный, т.к. DK - радиус в точку касания K
ΔBOC подобен ΔCKD по двум углам, прямому и общему ∠KCD

ΔBOC подобен ΔKPC по двум углам, прямому и общему ∠KCD

Длина окружности с центром в точке Р
L = 2π·KP = 2·π·2,4 = 4,8π
Ответ: радиус вписанного шара 3 мм;
длина линии касания 4,8π мм
Найти: r - ?; длину линии касания
Для решения нужно провести сечение конуса по диаметру основания, в сечении будет равнобедренный ΔBCA
ΔAOC - прямоугольный. По теореме Пифагора
OA² = AC² - h² = 100 - 64 = 36 = 6²
OA = 6 мм
ΔBCA равнобедренный ⇒ BA = 2·OA= 2·6 = 12 мм
Площадь треугольника
Площадь треугольника через радиус вписанной окружности
16r = 48 ⇒ r = 3 мм
Длина касания - это длина окружности
с центром в точке P и радиусом KP
ΔDKC - прямоугольный, т.к. DK - радиус в точку касания K
ΔBOC подобен ΔCKD по двум углам, прямому и общему ∠KCD
ΔBOC подобен ΔKPC по двум углам, прямому и общему ∠KCD
Длина окружности с центром в точке Р
L = 2π·KP = 2·π·2,4 = 4,8π
Ответ: радиус вписанного шара 3 мм;
длина линии касания 4,8π мм
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад