Question

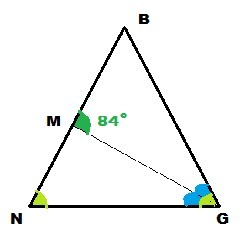
В равнобедренном треугольнике NBG проведена биссектриса GM угла ∠G у основания NG, ∠GMB = 84 градуса. Определите величины углов данного треугольника.

Answer 1

ΔNBG - равнобедренный  ⇒∠N = ∠BGN
GM - биссектриса  ⇒  ∠NGM = ∠BGM = 1/2 ∠BGN = 1/2 ∠N
∠N + ∠BGN + ∠B = 180°  ⇒  2∠BGN + ∠B = 180° ⇒
∠B = 180° - 2∠BGN

ΔBMG :  180° = ∠B + ∠BMG + ∠BGM
180° = 180° - 2∠BGN + 84° + 1/2 ∠BGN
1,5∠BGN = 84°
∠BGN = 56°
∠N = ∠BGN = 56°
∠B = 180° - 2∠BGN = 180° - 2*56° = 68°

Ответ: в ΔBNG  ∠N=∠G= 56°;  ∠B = 68°

Answer 2

разъясни!