Помогите пожалуйста с показательными уравнениями. Там все степени
Просто напишите как а этих примерах выйти на простое показательное уравнение.
Приложения:
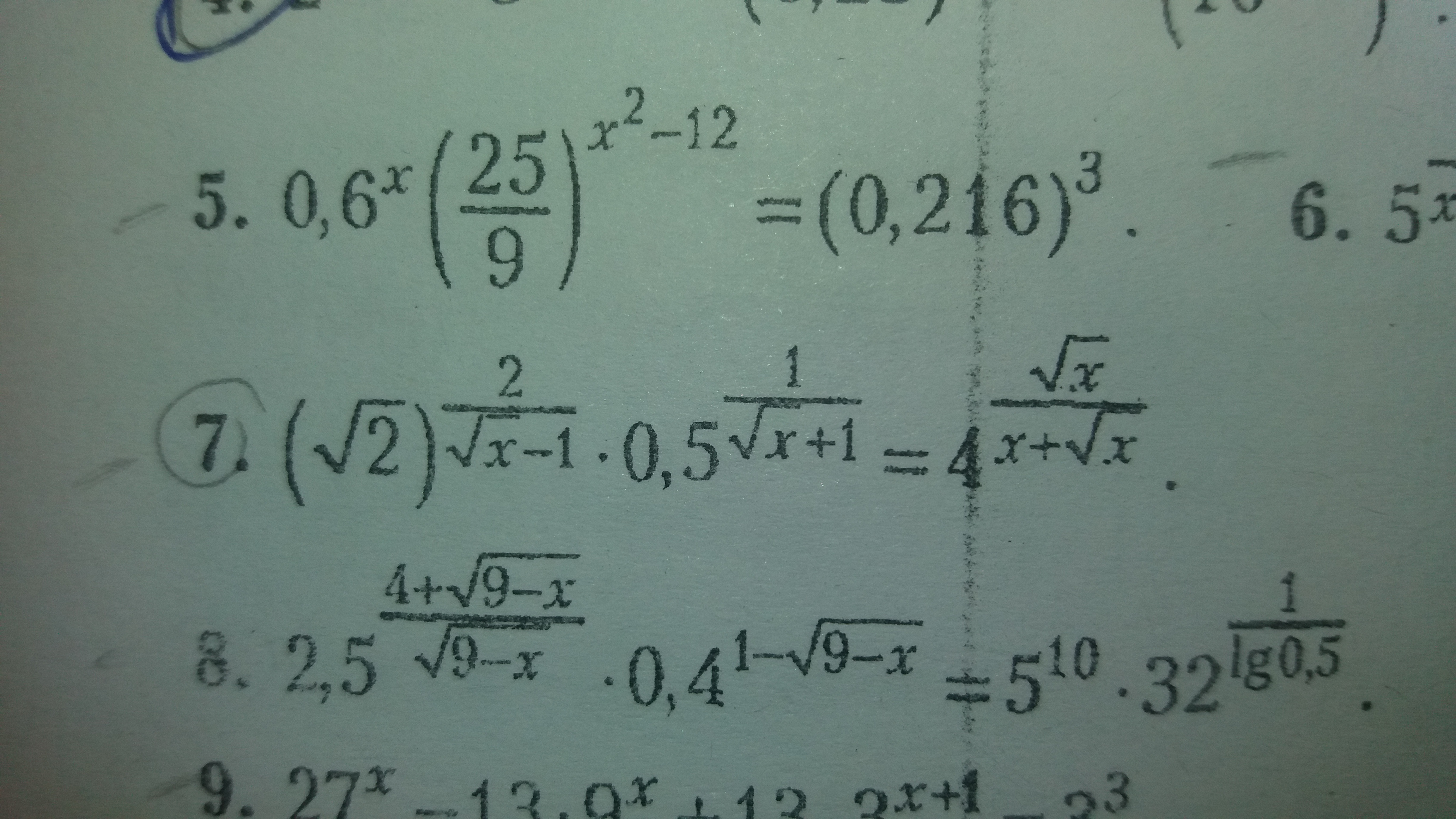
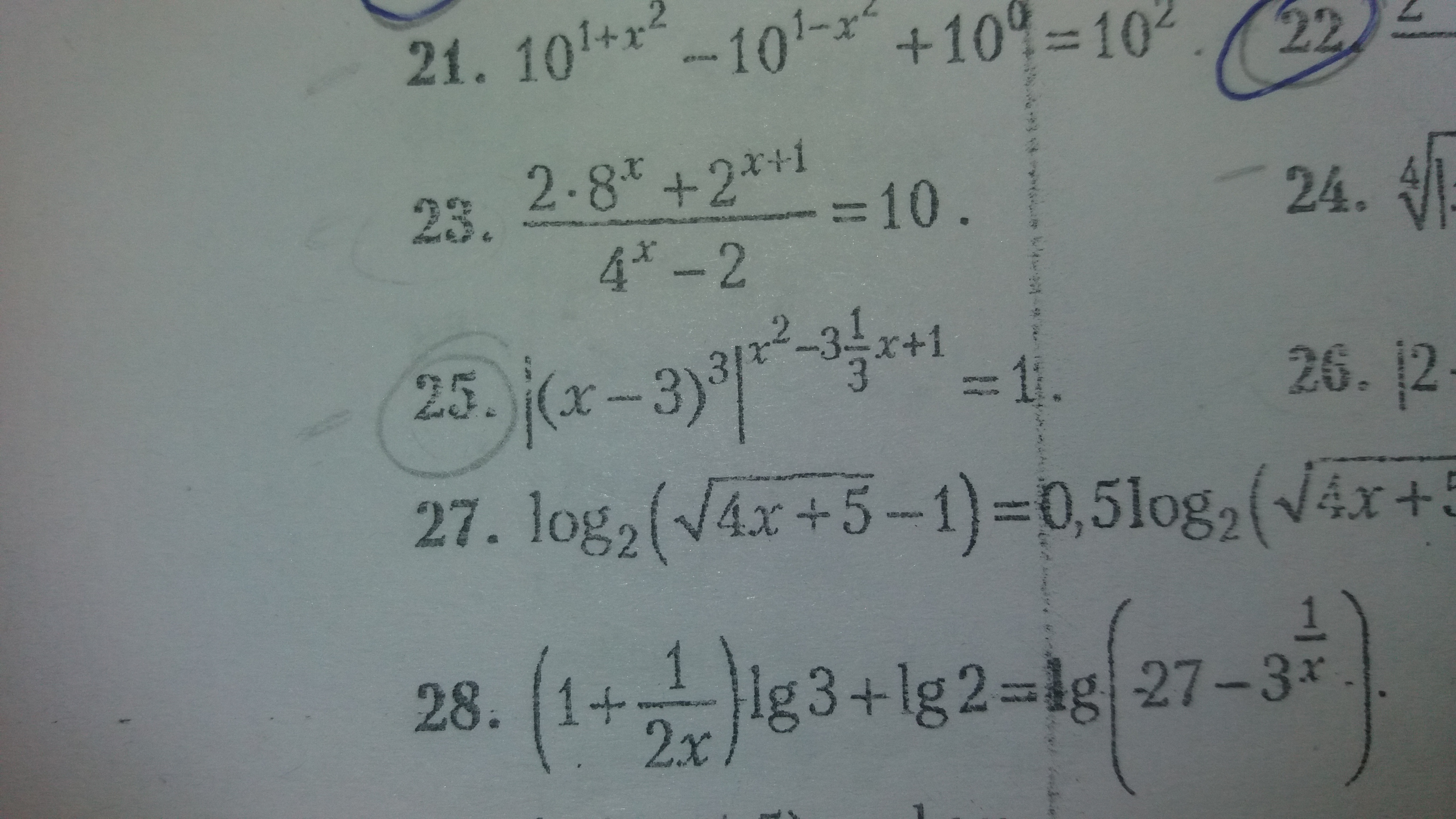

Ответы
Ответ дал:
0
1) Показатель во 2 числе

Числа перемножаются, значит, показатели складываются.

Основания одинаковые, значит, и показатели равны.

Знаменатель 2(1 + √x) > 0 при любом x, умножаем на него
x - √x - 2 = 7(1 + √x)
x - 8√x - 9 = 0
(√x + 1)(√x - 9) = 0
√x + 1 > 0 при любом x, поэтому корень
√x = 9
x = 81
7) Первое число слева

Второе число слева

Число справа

Слева умножение, значит, показатели складываются.
Основания одинаковые, значит, и показатели равны.

Область определения: x >= 0; x ≠ 1. Умножаем все на (√x - 1)(√x + 1) = x - 1
√x + 1 - (√x - 1) = 2(√x - 1)
2 = 2√x - 2
2√x = 4
x = 4
25) При x = 3 левая часть равна 0, поэтому это НЕ решение.
При x ≠ 3 показатель левой части равен 0
3(x^2 - (3 1/3)*x + 1) = 3(x^2 - 10/3*x + 1) = 0
3x^2 - 10x + 3 = 0
(x - 3)(3x - 1) = 0
Корень x = 3 не подходит, это мы уже выяснили.
x = 1/3
Числа перемножаются, значит, показатели складываются.
Основания одинаковые, значит, и показатели равны.
Знаменатель 2(1 + √x) > 0 при любом x, умножаем на него
x - √x - 2 = 7(1 + √x)
x - 8√x - 9 = 0
(√x + 1)(√x - 9) = 0
√x + 1 > 0 при любом x, поэтому корень
√x = 9
x = 81
7) Первое число слева
Второе число слева
Число справа
Слева умножение, значит, показатели складываются.
Основания одинаковые, значит, и показатели равны.
Область определения: x >= 0; x ≠ 1. Умножаем все на (√x - 1)(√x + 1) = x - 1
√x + 1 - (√x - 1) = 2(√x - 1)
2 = 2√x - 2
2√x = 4
x = 4
25) При x = 3 левая часть равна 0, поэтому это НЕ решение.
При x ≠ 3 показатель левой части равен 0
3(x^2 - (3 1/3)*x + 1) = 3(x^2 - 10/3*x + 1) = 0
3x^2 - 10x + 3 = 0
(x - 3)(3x - 1) = 0
Корень x = 3 не подходит, это мы уже выяснили.
x = 1/3
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад