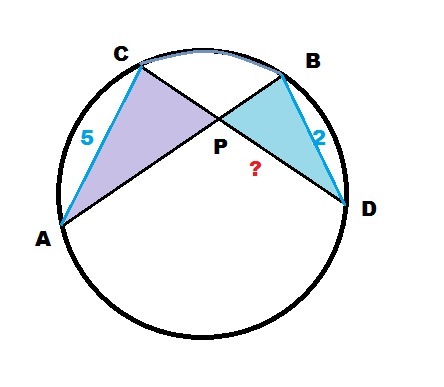
Известно, что хорды AB и CD пересекаются в точке P. Найдите PD, если известно, что AC=5, BD=2 и CD=14.
Ответы
Ответ дал:
0
CD = CP + PD = 14 ⇒ CP = 14 - PD
ΔACP и ΔDBP
∠CAB = ∠CDB - опираются на одну дугу CB
∠APC = ∠BPD - вертикальные ⇒ ΔACP подобен ΔDBP

5PD = 2(14 - PD)
5PD = 28 - 2PD
7PD = 28 PD = 4
ΔACP и ΔDBP
∠CAB = ∠CDB - опираются на одну дугу CB
∠APC = ∠BPD - вертикальные ⇒ ΔACP подобен ΔDBP
5PD = 2(14 - PD)
5PD = 28 - 2PD
7PD = 28 PD = 4
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад