Ответы
Ответ дал:
0
1. Скорость v(t) - это первая производная от зависимости координаты точки х от времени t - s(t). Поэтому, чтобы найти эту зависимость, надо взять интеграл от скорости.

Т.к. в начальный момент времени точка была в начале координат, то постоянная С находится путём подстановки:

Ответ: В
2. Первообразные от табличных функций:

Ответ: А
3. Первообразная:

На интервале функция f(x)=1/x отрицательна, первообразная ln(x) при этих значениях не существует, поэтому пишут:
функция f(x)=1/x отрицательна, первообразная ln(x) при этих значениях не существует, поэтому пишут:

Или, для указанного интервала можно записать:

Ответ: Б
4. Находим первообразную. Умножим и разделим подынтегральную функцию на 2. Затем двойку заносим под дифференциал. От этого ничего не меняется, т.к. d(2x) = 2dx. В этом случае аргумент функции (в данном случае синуса) будет совпадать с дифференциалом, и можно напрямую воспользоваться табличной первообразной синуса.

Первообразная проходит через точку (0; -1). Поэтому надо в полученную первообразную вместо икса подставить его значение (х=0) и приравнять значению первообразной (-1). Так мы найдём постоянную С.

Итак, искомая первообразная имеет вид:

Ответ: Б
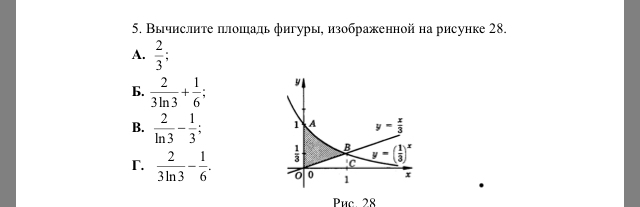
5. Из рисунка видно, что площадь фигуры ищется от нуля до единицы.
Закрашенную область можно вычислить так:
1) найти площадь фигуры, ограниченной кривой
2) найти площадь фигуры, ограниченной кривой
3) из первой площади вычитаем вторую.


Ответ: Г
Т.к. в начальный момент времени точка была в начале координат, то постоянная С находится путём подстановки:
Ответ: В
2. Первообразные от табличных функций:
Ответ: А
3. Первообразная:
На интервале
Или, для указанного интервала можно записать:
Ответ: Б
4. Находим первообразную. Умножим и разделим подынтегральную функцию на 2. Затем двойку заносим под дифференциал. От этого ничего не меняется, т.к. d(2x) = 2dx. В этом случае аргумент функции (в данном случае синуса) будет совпадать с дифференциалом, и можно напрямую воспользоваться табличной первообразной синуса.
Первообразная проходит через точку (0; -1). Поэтому надо в полученную первообразную вместо икса подставить его значение (х=0) и приравнять значению первообразной (-1). Так мы найдём постоянную С.
Итак, искомая первообразная имеет вид:
Ответ: Б
5. Из рисунка видно, что площадь фигуры ищется от нуля до единицы.
Закрашенную область можно вычислить так:
1) найти площадь фигуры, ограниченной кривой
2) найти площадь фигуры, ограниченной кривой
3) из первой площади вычитаем вторую.
Ответ: Г
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад