Question

167,168,169 под буквой a

Answer 1

167
одз:
x>0
решаем:
$a)4log_{4}{x}- frac{33}{log_{4}{x}} leq 1 \log_{4}{x}=y \4y- frac{33}{y} leq 1 \ frac{4y^2-33}{y} -1 leq 0 \ frac{4y^2-33-y}{y} leq 0 \4y^2-y-33 =0 \D=1+528=529=23^2 \y_1= frac{1+23}{8} =3 \y_2= frac{1-23}{8} =- frac{22}{8} =- frac{11}{4} \4(y-3)(y+ frac{11}{4} )=(y-3)(4y+11) \ frac{(y-3)(4y+11)}{y} leq 0$
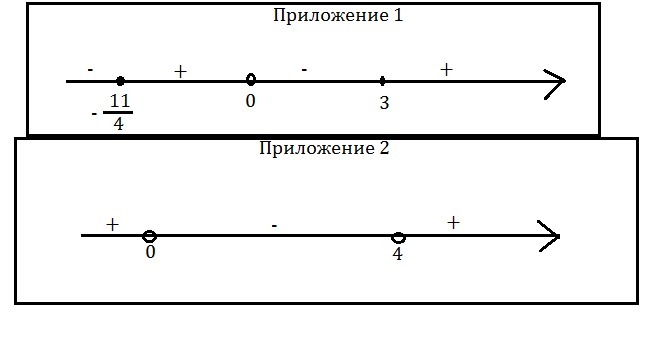
используем метод интервалов(см. приложение 1)
$y in (-infty;- frac{11}{4} ]cup (0;3]$
обратная замена:
$left[begin{array}{ccc}log_{4}{x} leq - frac{11}{4} \ 0 textless log_{4}{x} leq 3end{array}right. Rightarrow left[begin{array}{ccc}x leq frac{1}{sqrt[4]{4^{11}}} \ left{begin{array}{ccc}log_4{x} textgreater 0\log_4{x} leq 3end{array}right.end{array}right. Rightarrow left[begin{array}{ccc}x leq frac{1}{32sqrt{2}} \ left{begin{array}{ccc}x textgreater 1\x leq 64end{array}right.end{array}right.$
$left[begin{array}{ccc}x in (-infty; frac{sqrt{2}}{64}]\x in (1;64]end{array}right. Rightarrow x in(-infty; frac{sqrt{2}}{64}]cup (1;64]$
с одз:
$x in((-infty; frac{sqrt{2}}{64}]cup (1;64])cap (0;+infty)=(0;frac{sqrt{2}}{64}]cup (1;64]$
Ответ: $(0;frac{sqrt{2}}{64}]cup (1;64]$
168
одз: x>0
решаем:
$a) frac{1}{log_2{x}-4} textgreater frac{1}{log_2{x} } \log_2{x}=y \ frac{1}{y-4} - frac{1}{y} textgreater 0 \ frac{y-y+4}{y(y-4)} textgreater 0 \ frac{4}{y(y-4)} textgreater 0 \ y(y-4) textgreater 0$
решаем методом интервалов(см. приложение 2)
$y in (-infty;0)cup (4;+infty)$
обратная замена:
$left[begin{array}{ccc}log_2{x} textless 0\log_2{x} textgreater 4end{array}right. Rightarrow left[begin{array}{ccc}x textless 1\x textgreater 16end{array}right. Rightarrow xin (-infty;1)cup(16;+infty)$
теперь с одз:
$xin ((-infty;1)cup(16;+infty))cap (0;+infty)=(0;1)cup (16;+infty)$
Ответ: $x in (0;1)cup (16;+infty)$
169
одз:
x+1>0
x>-1
решаем:
$frac{log_{0,3}(x+1)}{log_{0,3}{100}-log_{0,3}{9}} textless 1 \ frac{log_{0,3}(x+1)}{log_{0,3}{ frac{100}{9} }}} textless 1 \frac{log_{0,3}(x+1)}{2log_{0,3}{ frac{10}{3} }}} textless 1 \frac{log_{0,3}(x+1)}{-2log_{0,3}{ 0,3 }}} textless 1 \log_{0,3}(x+1) textgreater -2 \-log_{ frac{10}{3} }(x+1) textgreater -2 \x+1 textless frac{100}{9} \x textless frac{91}{9} \x in (-infty;frac{91}{9} )$
с одз:
$x in (-infty;frac{91}{9} )cap (-1;+infty)=(-1;frac{91}{9} )$
Ответ: $xin (-1;frac{91}{9} )$