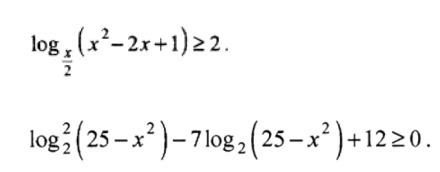Ответы
Ответ дал:
0
#1
Нахождение ОДЗ:




ОДЗ - (0;1)∪(1;2)∪(2;+∞)
Основание логарифма может принадлежать к двум промежуткам - (0;1) или (1;+∞). Найдем решение в каждом из случаев.
1)









Пересечение ОДЗ и решения дает нам интервал [2/3;1)∪(1;2)
2)








Пересечение ОДЗ и решения дает нам (2;+∞)
Объединение решений случаев 1 и 2 дает общее решение неравенства - [2/3;1)∪(1;2)∪(2;+∞)
#2
Нахождение ОДЗ:



ОДЗ - (-5;5)










(-∞;-√17]∪[√17;+∞)





[-3;3]
Объединение решений учетом ОДЗ (-5;5) - (-5;-√17]∪[-3;3]∪[√17;5)
Нахождение ОДЗ:
ОДЗ - (0;1)∪(1;2)∪(2;+∞)
Основание логарифма может принадлежать к двум промежуткам - (0;1) или (1;+∞). Найдем решение в каждом из случаев.
1)
Пересечение ОДЗ и решения дает нам интервал [2/3;1)∪(1;2)
2)
Пересечение ОДЗ и решения дает нам (2;+∞)
Объединение решений случаев 1 и 2 дает общее решение неравенства - [2/3;1)∪(1;2)∪(2;+∞)
#2
Нахождение ОДЗ:
ОДЗ - (-5;5)
(-∞;-√17]∪[√17;+∞)
[-3;3]
Объединение решений учетом ОДЗ (-5;5) - (-5;-√17]∪[-3;3]∪[√17;5)
Вас заинтересует
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад