Хорда основания цилиндра равна 16 см и удалена от центра этого основания на 6 см. Отрезок, соединяющий центр другого основания цилиндра с концом данной хорды, образует с плоскостью основания угол 45 градусов. Найдите объем цилиндра.
Ответы
Ответ дал:
0
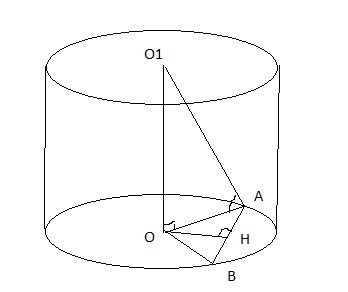
AB - хорда, AB = 16
O, O1 - центры соответственно нижнего и верхнего оснований.
OH - перпендикуляр к хорде AB, OH = 6
Соединим центры оснований высотой OO1
Т.к. OO1 ⊥ плоскости OAB, то OA - проекция наклонной O1A на плоскость OAB и ∠OAO1 и будет углом между наклонной O1A и плоскостью основания ⇒ ∠OAO1 = 45°
Из прямоугольного ΔOHA по теореме Пифагора:
Из прямоугольного ΔOAO1 (он равнобедренный, т.к. ∠OAO1 = 45°)
OO1 = OA = 10
Найдем объем цилиндра:
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад