Найти частное решение дифференциального уравнения удовлетворяющее начальным условиям.
Приложения:
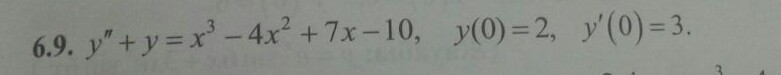
Ответы
Ответ дал:
0
6.9. 
Ищем общее решение Y однородного уравнения:

Характеристическое уравнение:

Имеем два сопряжённых комплексных корня характеристического уравнения:

тогда общее решение однородного уравнения имеет вид:

Подставляем наши значения:

Т.к. правая часть содержит степенную функцию, то частное решение ищем в виде:

Используем метод неизвестных коэффициентов, чтобы найти наши A, B, C, D, для чего предполагаемую функцию и её вторую производную подставляем в исходное уравнение:

Итак, частное решение такое:

Суммируем общее и частное решения Y + y:

Находим частное решение по начальным условиям:
y(0) = 2; y'(0) = 3
Находим производную:

Подставляем начальные значения в у и у'

Итак, требуемое решение выглядит так:

Ищем общее решение Y однородного уравнения:
Характеристическое уравнение:
Имеем два сопряжённых комплексных корня характеристического уравнения:
тогда общее решение однородного уравнения имеет вид:
Подставляем наши значения:
Т.к. правая часть содержит степенную функцию, то частное решение ищем в виде:
Используем метод неизвестных коэффициентов, чтобы найти наши A, B, C, D, для чего предполагаемую функцию и её вторую производную подставляем в исходное уравнение:
Итак, частное решение такое:
Суммируем общее и частное решения Y + y:
Находим частное решение по начальным условиям:
y(0) = 2; y'(0) = 3
Находим производную:
Подставляем начальные значения в у и у'
Итак, требуемое решение выглядит так:
Ответ дал:
0
Ответ такой
Ответ дал:
0
Да, всё верно. Если откроют для изменения, то перепишу.
Ответ дал:
0
https://znanija.com/task/27738004
Ответ дал:
0
Всё. Смотрите и там и тут.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
10 лет назад