Промежутки монотонности функций и точка экстремума
а) y=x^4-10^2+9
б)y=x^5-x^3+x+2
в)y=-7x^3+x^2-3x-1
Ответы
Ответ дал:
1
ДУМАЕМ
Находим корни производной - там точки экстремума.
Производная положительная - функция убывает и наоборот.
РЕШЕНИЕ
а)
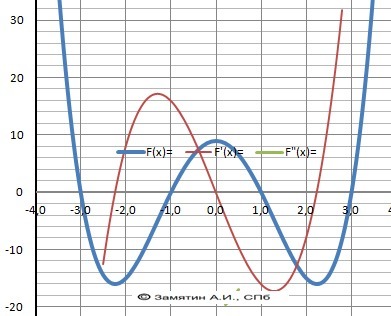
y(x) = x⁴-10*x²+9
Производная
y'(x) = 4*x³ - 20*x = 4x*(x²-5) = 0
Находим корни производной - точки экстремумов.
x₁ = 0, x₂.₃ = +/- √(5 ≈ +/- 2.24 - ОТВЕТ - рис. 1..
б)
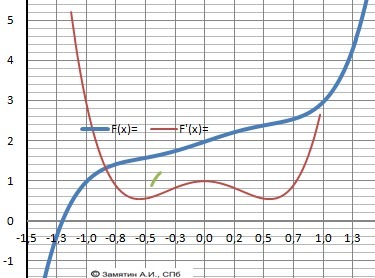
y(x) = x⁵ - x³ - x + 2
y'(x) = 5*x⁴ - 3*x² - 1
Корней нет - экстремумов - нет. Возрастает на всём интервале существования. Рис. 2.
в)
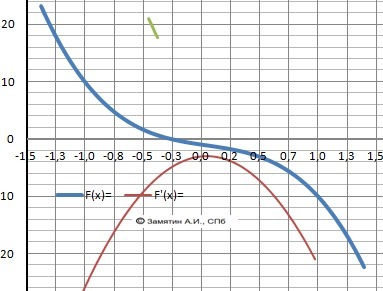
y(x) = -7*x³ + x² - 3*x - 1
y'(x) = - 21*x² + 2*x - 3
Корней нет - нет экстремумов - рис. 3.
Рисунки с графиками функций - в приложении.
Находим корни производной - там точки экстремума.
Производная положительная - функция убывает и наоборот.
РЕШЕНИЕ
а)
y(x) = x⁴-10*x²+9
Производная
y'(x) = 4*x³ - 20*x = 4x*(x²-5) = 0
Находим корни производной - точки экстремумов.
x₁ = 0, x₂.₃ = +/- √(5 ≈ +/- 2.24 - ОТВЕТ - рис. 1..
б)
y(x) = x⁵ - x³ - x + 2
y'(x) = 5*x⁴ - 3*x² - 1
Корней нет - экстремумов - нет. Возрастает на всём интервале существования. Рис. 2.
в)
y(x) = -7*x³ + x² - 3*x - 1
y'(x) = - 21*x² + 2*x - 3
Корней нет - нет экстремумов - рис. 3.
Рисунки с графиками функций - в приложении.
Приложения:
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
9 лет назад