Question

log 3x²+7x+1 по основанию (x-3)² ≥0

Answer 1

У логарифмов есть свойство:
$log_a(b)= \frac{log_c(b)}{log_c(a)}$
Причем новое основание с может быть каким угодно, лишь бы c>0 и c≠1.
В нашем случае
$log_{(x-3)^2}(3x^2+7x+1) = \frac{lg(3x^2+7x+1)}{lg(x-3)^2} \geq 0$
Область определения:
{ x ≠ 3; x ≠ 4; x ≠ 2; при всех остальных х будет (x-3)^2 > 0 и не = 1.
{ 3x^2 + 7x + 1 > 0
D = 7^2 - 4*3*1 = 49 - 12 = 37
x1 = (-7 - √37)/6 ≈ -2,18
x2 = (-7 + √37)/6 ≈ -0,15
Область определения:
x ∈ (-oo; (-7 - √37)/6) U ((-7 + √37)/6; 2) U (2; 3) U (3; 4) U (4; +oo)
Теперь решаем само неравенство:
$\frac{lg(3x^2+7x+1)}{lg(x-3)^2} \geq 0$
Если дробь равна 0, то числитель равен 0
$lg(3x^2+7x+1)=0$
3x^2 + 7x + 1 = 1
3x^2 + 7x = 0
x1 = -7/3; x2 = 0

Если дробь > 0, то числитель и знаменатель имеют одинаковые знаки.
1)
{ $lg(3x^2+7x+1) \leq 0$
{ $lg(x-3)^2 \ \textless \ 0$
0 = lg 1, поэтому переходим от логарифмов к числам под ними
{ 3x^2 + 7x + 1 ≤ 1
{ (x - 3)^2 < 1
Раскрываем скобки и приводим подобные
{ 3x^2 + 7x ≤ 0
{ x^2 - 6x + 9 - 1 < 0
Раскладываем на скобки
{ x(3x + 7) ≤ 0
{ (x - 2)(x - 4) < 0
Получаем
{ x ∈ [-7/3; 0]
{ x ∈ (2; 4)
Эти промежутки не пересекаются, поэтому решений нет.

2)
{ $lg(3x^2+7x+1) \geq 0$
{ $lg(x-3)^2 \ \textgreater \ 0$
Переходим от логарифмов к числам под ними
{ 3x^2 + 7x + 1 ≥ 1
{ (x - 3)^2 > 1
Раскрываем скобки и приводим подобные
{ 3x^2 + 7x ≥ 0
{ x^2 - 6x + 9 - 1 > 0
Раскладываем на скобки
{ x(3x + 7) ≥ 0
{ (x - 2)(x - 4) > 0
Получаем
{ x ∈ (-oo; -7/3] U [0; +oo)
{ x ∈ (-oo; 2) U (4; +oo)
Пересечение этих промежутков:
x ∈ (-oo; -7/3] U (4; +oo)
Теперь смотрим область определения.
(-7 - √37)/6 ≈ -2,18 > -7/3; точки 2, 3 и 4 вообще выпадают из промежутков, поэтому область определения на ответ не влияет.
Ответ: x ∈ (-oo; -7/3] U [0] U (4; +oo)

Answer 2

Mefody66 почти всё верно решил, за исключением одного промежутка определения функции.

Да, точка х = 2 выпадает их области, но промежуток 0 <= x <2 остаётся.
Поэтому ответ:
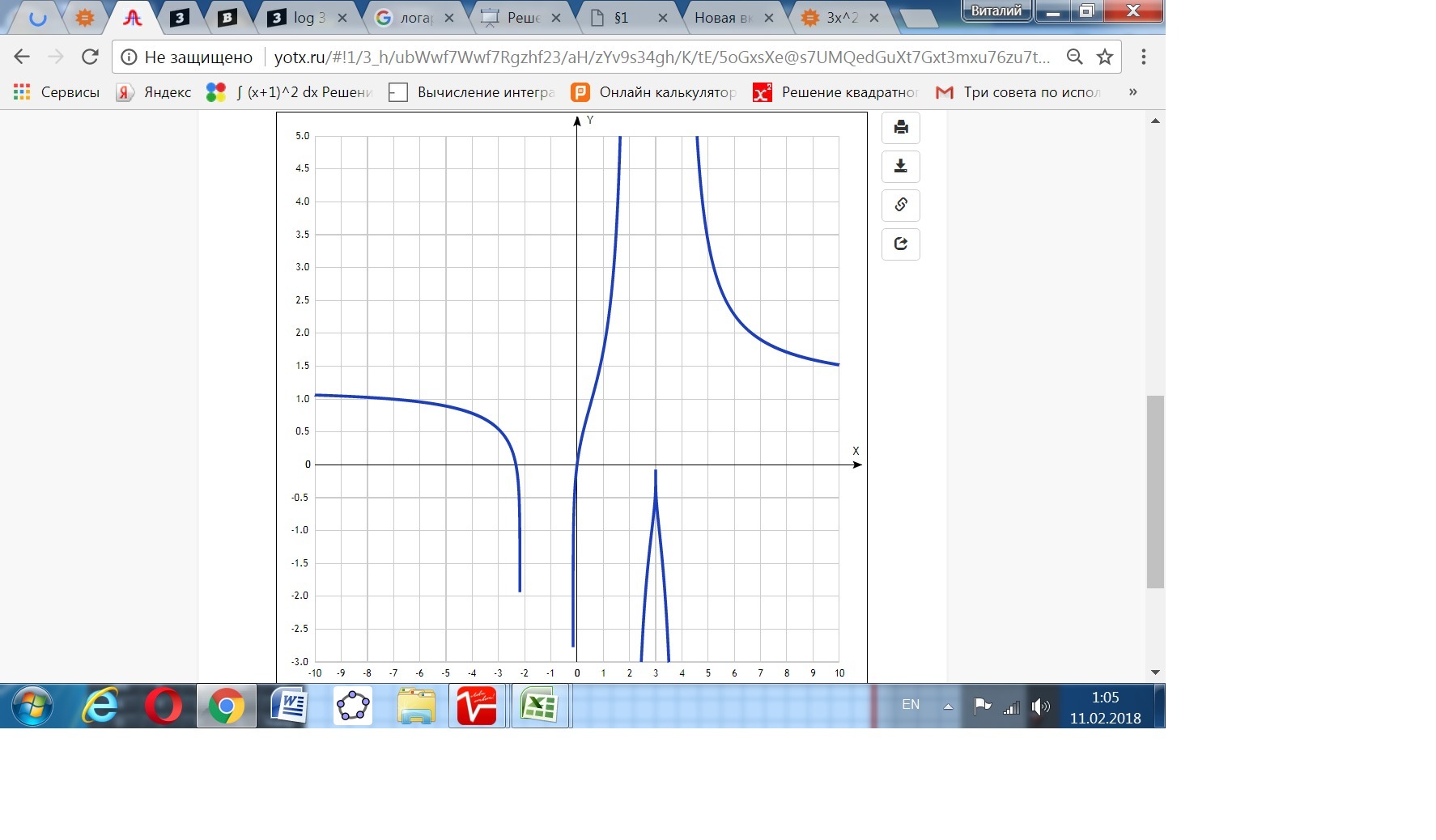
x ∈ (∞; (-7/3)]∪[0; 2)∪(4; +∞).
Или в другой записи:
x ≤ (-7/3),
0 ≤ x <2,
x > 4.
На прилагаемом графике функции эти промежутки хорошо видны.