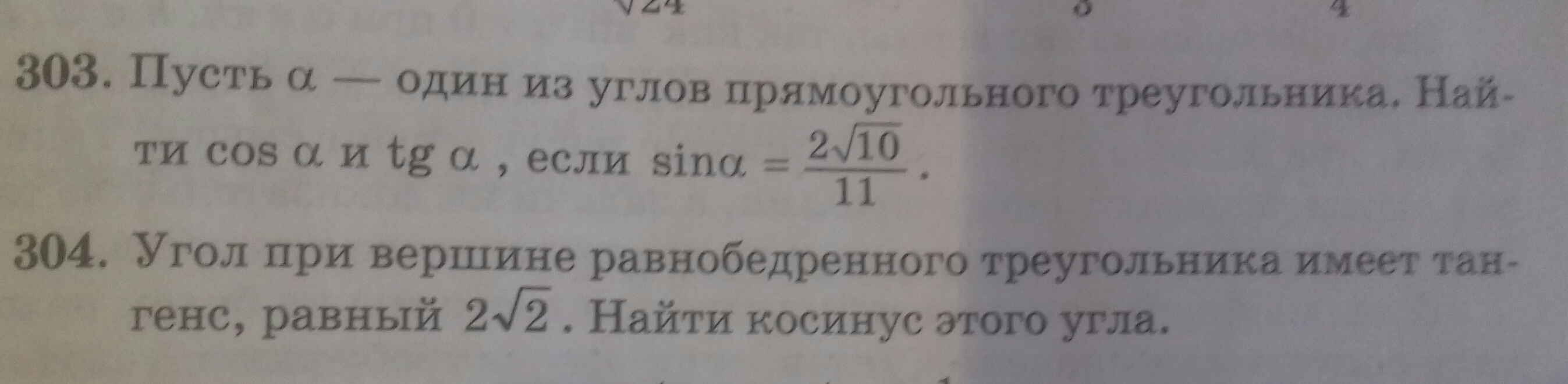Ответы
Ответ дал:
0
303
у прямоугольном треугольнике один угол прямой, остальные - острые => их синусы, косинусы, тангенсы будут положительными.
воспользуемся следующими формулами:

применим их:

Ответ:
304
воспользуемся следующим тождеством:

теперь определим знак косинуса:
если тангенс этого угла положительный => данный угол находится в 1 или 3 четверти. Но так как сумма углов треугольника не превышает 180°, а в 3 четверти углы от 180° до 270° - 3 четверть не подойдет, остается только 1 четверть, а в ней косинус положительный =>
Ответ: 1/3
у прямоугольном треугольнике один угол прямой, остальные - острые => их синусы, косинусы, тангенсы будут положительными.
воспользуемся следующими формулами:
применим их:
Ответ:
304
воспользуемся следующим тождеством:
теперь определим знак косинуса:
если тангенс этого угла положительный => данный угол находится в 1 или 3 четверти. Но так как сумма углов треугольника не превышает 180°, а в 3 четверти углы от 180° до 270° - 3 четверть не подойдет, остается только 1 четверть, а в ней косинус положительный =>
Ответ: 1/3
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад