Question

Сделайте 2,3,4. Спасибо.

Answer 1

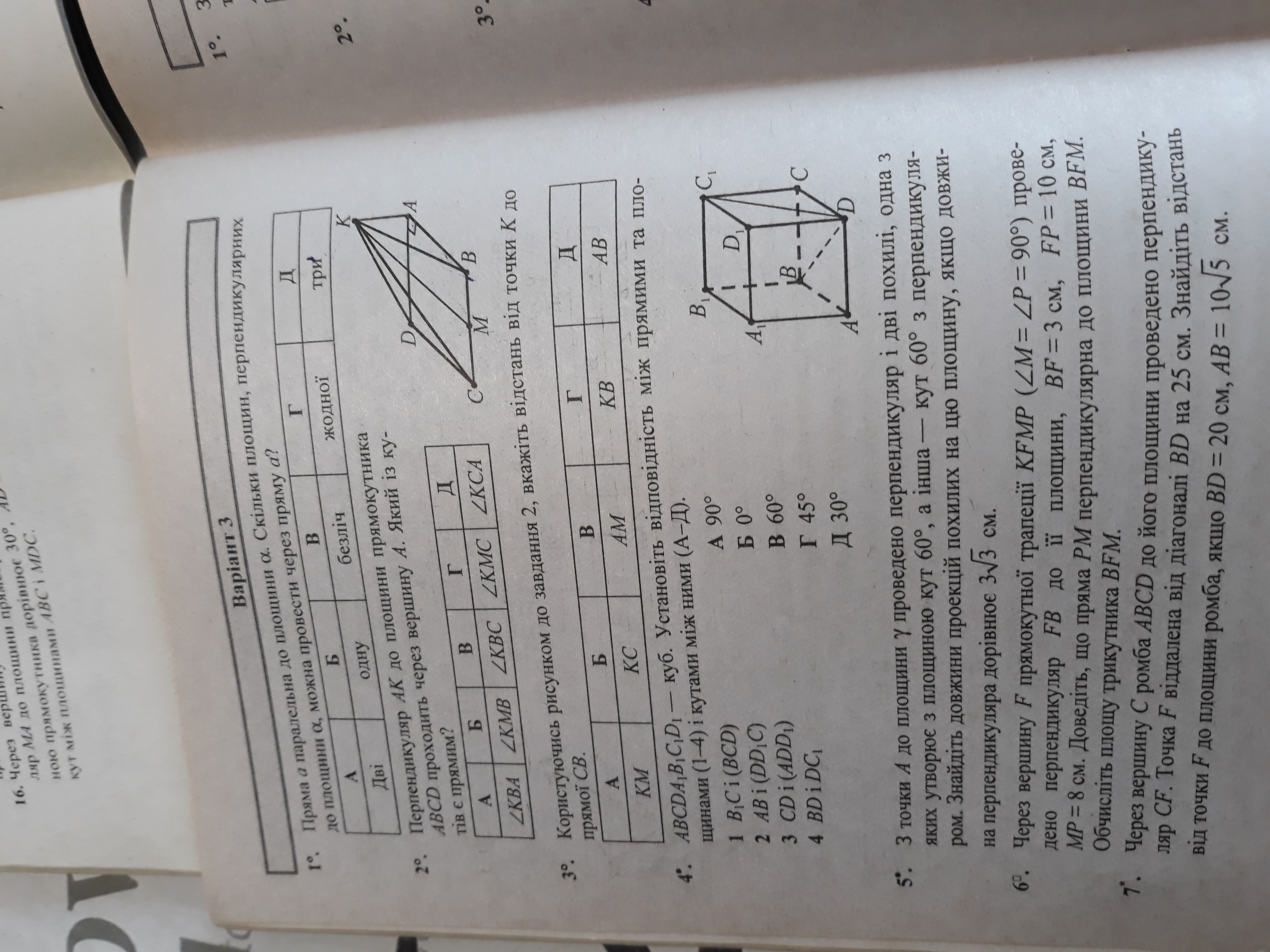
2. По теореме о трех перпендикулярах <KBC=90, так как АВ⊥ВС(АВСD - прямоугольник), а АВ - проекция наклонной КВ.
3. Расстояние от точки К до прямой СВ - это перпендикуляр КВ к прямой ВС.
4. Угол между В1С и плоскостью ВСD =45°, так как углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость, а это <B1CB - угол меду стороной и диагональю квадрата.
   Угол между АВ и плоскостью DD1С =0°, так как прямая АВ параллельна прямой DC (противоположные стороны квадрата), лежащей в плоскости DD1C.
   Угол между СD и плоскостью АDD1 =90°, так как прямая CD перпендикулярна пересекающимся прямым АD и DD1 (ребра куба), лежащим в плоскости АDD1.
   Угол между пересекающимися в точке D прямыми ВD и DC1 - <АDD1 =60°, так как эти прямые - стороны равностороннего треугольника BDC1.